Genetic variation in populations described by genotype & allele frequencies
            (not "gene" frequencies) 

Consider a diploid autosomal locus with two alleles & no dominance
      (=> semi-dominance: AA , Aa , aa  phenotypes distinguishable)

      x = # AA             y = # Aa             z = # aa         so that   x + y + z = N (sample size)

      f(AA) = x / N       f(Aa) = y / N       f(aa) = z / N

      f(A) = (2x + y) / 2N          f(a) = (2z + y) / 2N

            or    f(A) = f(AA) + 1/2 f(Aa)      f(a) = f(aa) + 1/2 f(Aa)

            let p = f(A), q = f(a)    p & q are allele frequencies 

      Properties of p & q

        p + q = 1     p = 1 - q    q = 1 - p

            (p + q)²  =  p² + 2pq + q²  =  1

            (1 - q)² + 2(1 - q)(q) + q² = 1

        p & q interchangeable wrt [read, "with respect to"] A & a

        q typically used for
                  rarer, recessive, deleterious (disadvantageous), or "interesting" allele

              BUT   'common' & 'rare' are statistical properties
                         'dominant' & 'recessive' are genotypic properties
                         'advantageous' & 'deleterious' are phenotypic properties
                  *** any combination of these properties is possible ***

What happens to p & q in one generation of random mating?

Consider a population of monoecious organisms that reproduce by random union of gametes
       (sea urchin / "tide pool" model)

      (1) Determine expectation
                 of parental alleles coming together in various genotype combinations
                 expectation: the anticipated value of a variable
                                       not quite the same as probability
            Proofs by probability, binomial expansion, & Punnet Square methods
            all show that expectation of f(AA) = p²
                                 expectation of f(Aa) = 2pq
                                 expectation of f(aa) = q²

     (2) Re-describe offspring allele frequencies f(A') & f(a')  

       f(A') = f(AA) + 1/2 f(Aa)
                    = p² + (1/2)(2pq) = p² + pq = (p)(p+q) = p' = p
 

       f(a') = f(aa) + 1/2 f(Aa)
                    = q² + (1/2)(2pq) = q² + pq = (q)(p+q) = q' = q

     p² : 2pq : q² are Hardy-Weinberg expectations (cf. Mendelian ratios 1 : 2 : 1 )

      Hardy-Weinberg Expectation (HWE) obtained under more general conditions

            (1) multiple alleles / locus

                  p + q + r = 1
                  (p + q + r)² = p² + 2pq + q² + 2qr + r² + 2pr = 1

                  Proportion of heterozygotes (H = 'heterozygosity')
                         measures genetic variation at a locus

              H_obs = f(Aa) = observed heterozygosity
              H_exp = 2pq   = expected heterozygosity (for two alleles)

              H_e = 2pq + 2pr + 2qr = 1 - (p² + q² + r²)    for three alleles

                                n
                  H_e = 1 -  (q_i)²      for n alleles
                               i=1

                        where q_i = freq. of i th allele of n alleles at a locus
 
             Ex.: if q₁ = 0.5, q₂ = 0.3, & q₃ = 0.2
                            then H_e = 1 - (0.5² + 0.3² + 0.2²) = 0.62

            *** HOMEWORK:
                     Calculate H_e 1) if q₁ = 0.4, q₂ = 0.3, q₃ = 0.2, & q₄ = 0.1
                                              2) for a locus with 10 or 100 alleles, all at equal frequency
                                           3) with one allele at q = 0.5, and 9 or 99 at equal frequency
                                                    Hint: is there a shortcut? 

            (2) sex-linked loci
                    iff [read: "if and only if"] allele frequencies in males & females equal
                    If frequencies initially unequal, they converge over several generations

            (3) dioecious organisms
                    sexes separate
                    HWE produced by random mating of individuals
                        expand (p² 'AA' + 2pq 'AB' + q² 'BB')² :
                               nine possible mating types among genotypes
                    selfing (self-fertilization) remains possible

Genotype proportions in natural populations can be tested for HWE
     H_o (null hypothesis): no other phenomena acting
     Note:  HWE often called a HW equilibrium, BUT
                HWE observed only at time_o of any single generation
                         changes bx newborns & adults due to other factors
                HWE may be observed at time₁ with new p" and q"
           => HWE not an "equilibrium"

    Ex.: MN blood groups in Homo

      Among Euro-Americans:

MM	MN	NN	Sum
1787	3039	1303	6129

        f(M) = [(2)(1787) + 3039] / (2)(6129) = 0.539

        f(N) = [(2)(1303) + 3039] / (2)(6129)  = 0.461    = 1.0 - 0.539

     Chi-square (χ²) test:

	N genotypes	#	Observed	Expected	(obs-exp)	d2/exp
MM	p2N	(0.539)2(6129)	1787	1781	6	0.020
MN	2pqN	(2)(0.539)(0.461)(6129)	3039	3046	-7	0.012
NN	q2N	(0.461)2(6129)	1303	1302	1	0.000
			6129	6129	χ2 =	0.032ns

(cf. critical value p_{.05[2 df]} = 5.99)                               ( p >> 0.05)
 
      Use two degrees of freedom, because there are three observed classes,                                                  

         Chi-square test on combined data:

	Obs	Exp	d=(O-E)	d2/Exp
MM	327	195	132	89.35
MN	268	532	-264	131.01
NN	496	364	132	47.87
			χ2 =	268.23***

                                                                                  (p << 0.001)

      *=> A mixture of populations, each of which conforms to HWE,
            will not show expected HW proportions
            if allele frequencies differ in the separate populations.

      Wahlund Effect: Separate populations treated as one will be deficient in heterozygotes

                    (Basis of F statistics & population structure, later on)

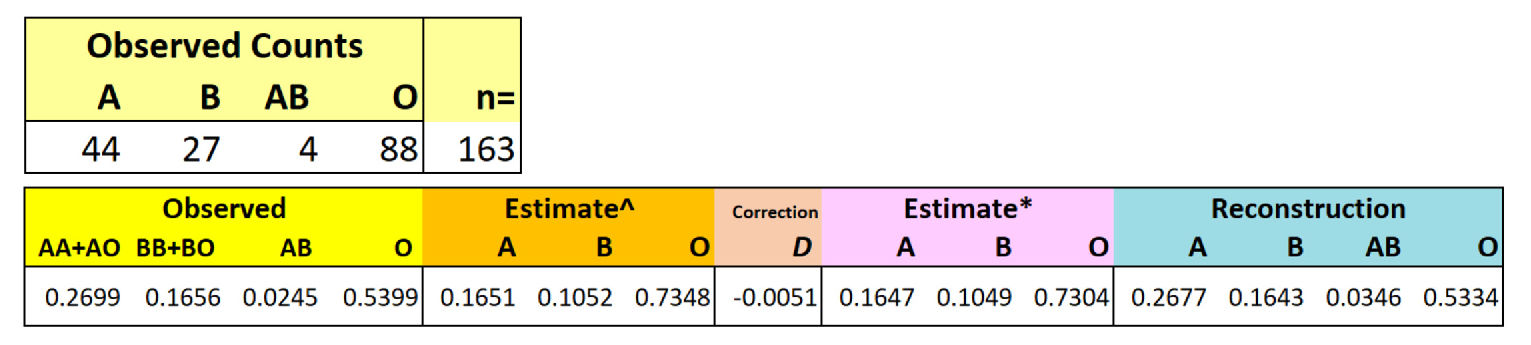
        Three alleles (A, B, O) produce
            six genotypes (AA, AO, BB, BO, AB, OO) with
                four phenotypes ("A", "B", "AB" "O")
                        A & B dominant to O; "A" = AA + AO; "B" = BB + BO
                        A & B" co-dominant as "AB"

Challenge: Cannot obtain exact algebraic solution for four phenotypes from three variables
                    Therefore use Likelihood method with correction
            Ex.: Best a priori likelihood estimate of f(O) is observed [f("O")]

Data from Aka (Mbenga) (Central African Republic) (Cavalli-Sforza & Bodmer 1971)

Hardy-Weinberg Expectation offers 'null hypothesis':
      Consequences of other genetic / evolutionary phenomena?

     Five major, interacting factors:

      1. Natural selection
            Change of allele frequencies (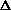q) [read 'delta q']
                  occurs due to differential effects of alleles on 'fitness'
            Consequences depend on dominance of fitness
                    [See hardy-weinberg.m MATLAB laboratory exercise]
            Natural Selection is the principle concern of micro-evolutionary theory

      2. Mutation
             New alleles arise at some rate µ
             If µ(AA')    µ'(AA'), net change in frequency

      3. Gene flow
            Movement of alleles between populations at some rate m
            (Im)migration introduces new alleles, changes frequency of existing allele

      4. Statistical sampling error
            Chance fluctuations occur in finite populations, especially with small N 
            Genetic drift: random change of allele frequencies
                                   over time and (or) space, within and (or) among populations
            Modification of N from non-random reproduction: variable sex ratio, offspring number, population size, etc.

      5. Population structure
           Inbreeding: preferential mating of relatives at some rate F
                Inbreeding modifies genotype proportions but not allele frequencies
           Assortative Mating: differential mating of phenotypes and (or) genotypes
           Meta-population structure: sub-populations differ wrt total population (F-statistics)