Migration-Selection equilibrium

Migration (Gene Flow) / Selection equilibrium

Consider island adjacent to mainland, with unidirectional migration from mainland to island.
   Mainland uniformly dark, island uniformly light
   AA phenotypes are light, BB dark, and AB intermediate
   Phenotypes subject to selection according to degree of crypsis

Fitness of AA, AB, & BB genotypes differ between environments,
      so allele frequency q = f(B) differs between mainland (q_m) & island (q_i)
      B has high fitness on mainland, low fitness on island
    For this model, A semi-dominant to B:
            B allele additive: W_AB = (1 - t)    W_BB = (1 - 2t)
            [Note: use t so as not to confuse additive vs recessive s]

	W_AA	W_AB	W_BB	q_init
Island	1	1 - t	1 - 2t	q_i 0
Mainland	0	0	1	q_m 1

Migration rate m = fraction of island population newly arrived from mainland
[m equivalent to fraction of new alleles arriving from mainland]

Migration / Selection equilibrium resemble Mutation / Selection equilibrium mathematically, except
Migration introduces alleles two at once (BB diploid migrants vs AB gametic mutations)
Migration rates m >> Mutation rates u

Calculate equilibrium frequency where q_i= f(B) = 0 on island:
     Change in f(B) from migration: q_i= m(q_m - q_i)
     Change in f(B) from selection: q_i = -tq_i(1 - q_i)) / (1 - 2tq_i)
                                                             -tq_i(1 - q_i)                    [if tq_i<< 1]
     Then, combined change          q_i= m(q_m - q_i) - tq_i(1 - q_i)
                                                            = mq_m - mq_i - tq_i + tq_i²)
                                                            = tq_i² - (m + t)(q_i) + mq_m

For q_i= 0   solve as quadratic equation for several special cases:

       if m    t:      q_iq_m              migration behaves like mutation
                                                                 [except: alleles introduced at higher rate, as diploids]

       if m >> t:      q_iq_m                 mainland B allele 'swamps' island A allele

       if m << t:      q_i (m / t)(q_m)     some equilibrium achieved, iff m constant

Intermediate cases can be simulated in GSM worksheet

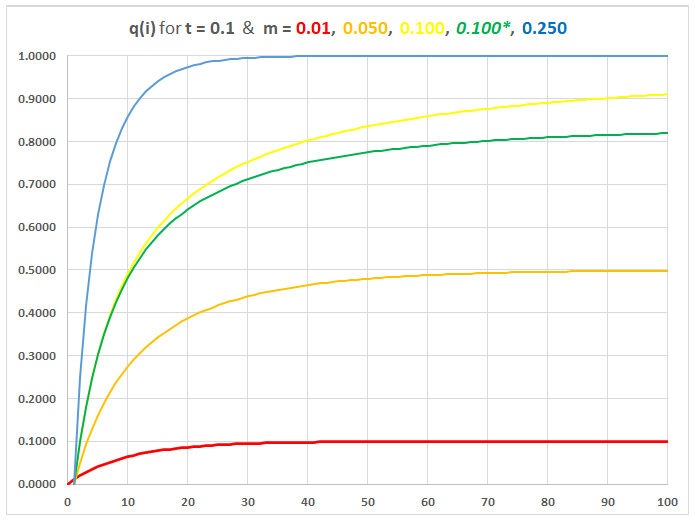
Mutation-Selection equilibrium

Approach to Mutation-Selection Equilibrium where q_i= 0
for t = 0.1 & m = 0.01 ~ 0.250

For m = 0.250, q_I rapidly approaches g_M: migration from the Mainland swamps locally favored allele, prevents local adaptation.

For m = 0.01 or 0.05, q_I reaches equilibrium at (m / t) as predicted: deleterious mainland allele maintained at relatively high frequency.

For m = t = 0.1, the approximate solution m = 0.1 underestimates an equilibrium q_M.
The exact solution with m = 0.1* is substantially higher, but takes much longer to achieve.