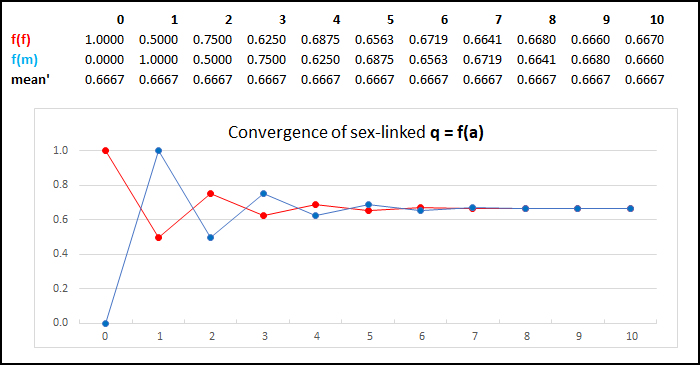
Approach to Hardy-Weinberg Proportions at sex-linked loci

    Consider a sex-linked locus in a species where females are XX (homogametic) and males are XY (heterogametic). Suppose f(a) is initially unequal in females and males, with f(a)_f = 1.0 and f(a)_m = 0.0.  (1) Because each female receives an X chromosome from both parents in generation n, the female f(a) in generation n+1 is the mean of the male and female f(a) in generation n. (2) Because each male in receives an X chromosome only from the female parent in generation n, the frequency of the allele f(a) in females of generation n determines f(a) in males in generation n+1. The male f(a) therefore "chases" the female f(a) in the preceding generation until they reach approximate equality.

    In this example, note that frequencies are within 1% of each other in the seventh generation, even when the initial frequencies are completely divergent.

    In the special case above, the mean f(a) for a sex-linked locus is a constant  [(2 x f(a)  +  1 x f(a)) / 3 ]. Thus the initial f(a) = (2 x 1 + 1 x 0) = 0.6667 and remains constant, even though it varies between sexes.

HOMEWORK: Suppose initial f(a) = 0.0 in females, and f(a) = 1.0 in males [The reverse of the graph above]. Calculate & graph the expected allele and genotype frequencies in males & females over the first seven generations.