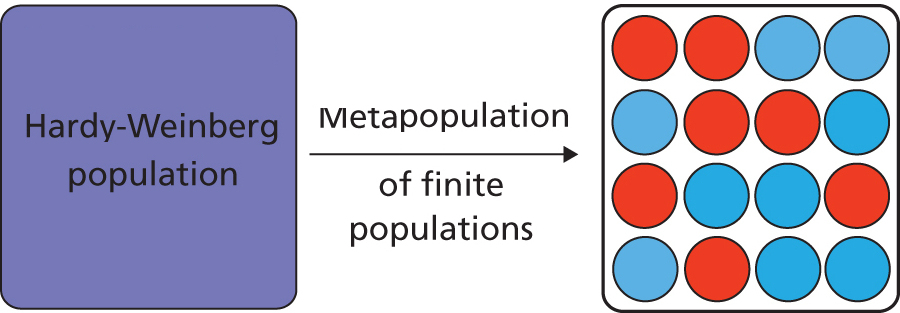
Prelude to population structure: a thought experiment

In a single infinitely large population not subject to selection, the expectation from the Hardy-Weinberg theorem is that allele and genotype frequencies will remain constant. When an infinite population is divided into a structured meta-population of smaller finite isolated populations, genetic drift ensures that each sub-population will eventually become fixed for one of the alleles originally present. In a two-allele system with p = (1 - q) = f(A₁) and (1 - p) = q = f(A₂), a fraction (1 - q) of the sub-populations will become fixed for A₁, and a fraction q fixed for A₂. The overall allele frequencies are the same in the ideal population and the meta-population, but the fraction of heterozygotes in the meta-population goes to 2pq = 0 over time. The deficiency of heterozygotes is thus a measure of population structure.