Extend single-locus  multilocus  quantitative models

      p²:2pq:q²                      W₀,W₁,W₂          Mendel & H-W Theorem
                                                                           
 normal distribution       fitness function     Heritability

Quantitative genetics: Variation can be quantified

       mean  standard deviation: 
      variance: ²

      Quantitative variation follows "normal distribution" (bell-curve) iff [read: "if and only if"]
              Multiple loci involved
              Each locus contributes equally (variance is additive)
              Each locus acts independently:
                    interaction variance ( σ²_GxE ) minimal

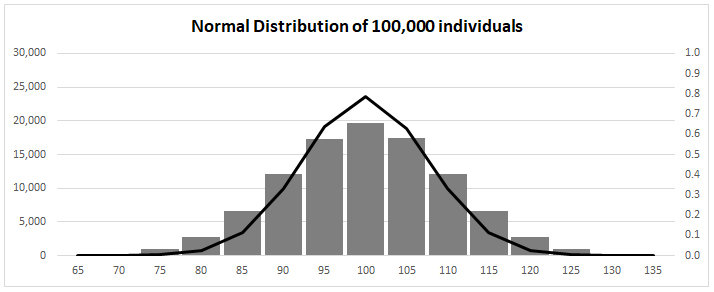
                                       Normal Distribution for Mean 100 10$$

Phenotypic variation has two sources: genetic (σ²_G) & environmental (σ²_E$$) variance$$$$$$$$

      phenotypic variance     σ²_P = σ²_G + σ²_E + σ²_GxE
      additive variance           σ²_A = σ²_G + σ²_E
      heritability                      h²  = σ²_G$$/ σ²_A  = σ²_G / (σ²_G + σ²_E)

           h² : "Heritability in the narrow sense": ignores _GxE²  =  interaction variance:
           Identical genotypes produce different phenotypes in different environments.
               Ex.: same breed of cows produces different milk yield on different feed
           Norm of Reaction for differential expression within & between environments

Artificial breeding indicates that organismal phenotypic variation is highly heritable
      ex.: Darwin's pigeon breeding experiments
             Artificial selection on agricultural species
                  Commercially useful traits improved by selective breeding
             IQ scores in Homo: h²  ~ 0.7
                   But: IQ scores improve with education: σ²_GxE$$is large
            Offspring / Mid-parent correlation

Fitness function expresses relationship between genotype & fitness
    A continuous variable over range of genotypes, rather than discrete values for W₀, W₁, & W₂

Most traits variable & heritable
          Many traits do respond to 'artificial' selection (h²  = 0.5 ~ 0.9)
          Many traits should respond to 'natural' selection

To demonstrate & measure Natural Selection in Nature,
         Show experimentally that heritable variation has consequences for fitness

       What happens to a normal distribution under Selection?
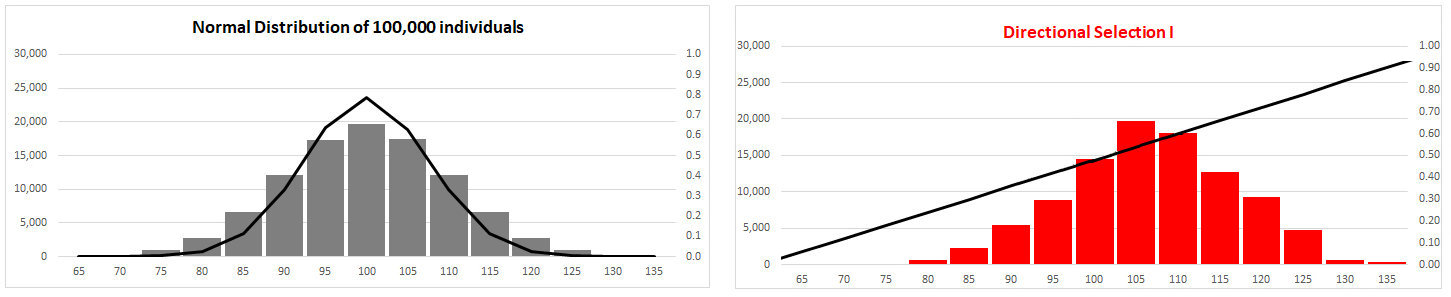
             Compare distributions before [left] and after [right] selection

Directional Selection
      (I) Fitness function has constant slope:
           Trait mean shifted towards one extreme of phenotype
            trait variance changed [skewed to right]
            NB: Fitness function resembles that for favored single allele
                   Variance corrected by HWE each generation

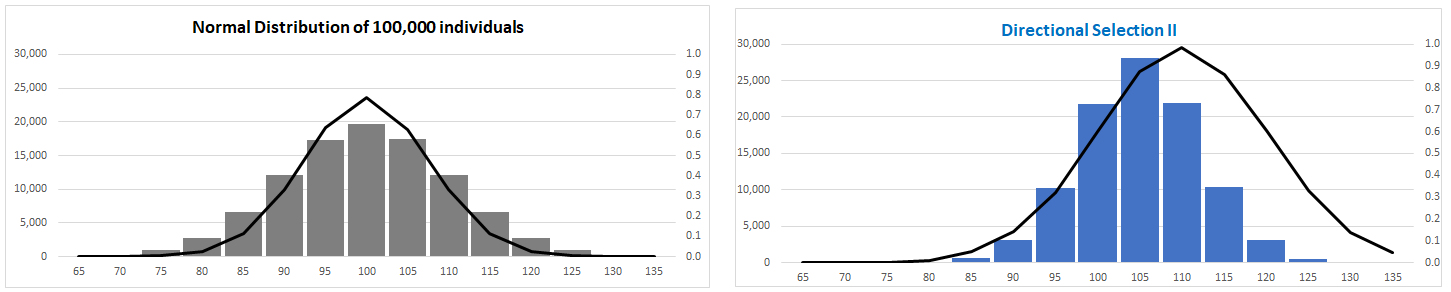
      (II) Fitness function normally distributed
           Trait mean shifted gradually: variance unaffected
           NB: Fitness function resembles that for heterozygote superiority:
                    What's different?

HOMEWORK: Compare and contrast predictions of single-locus versus multi-locus selection.

     In single-locus models, limit of selection is
      Elimination of variation by fixation of favored allele

    Clinal variation of B allele in human ABO system: f(B) declines East to West

    In quantitative models, rate limited by
       substitutional genetic load:
           Fitness "cost" (lost reproductive potential) to replace disadvantageous allele
 

        Substitutional Load = cumulative N over time as q 0

   "Soft" selection
          Mortality is density-dependent
               N_(after)  ~ N_(before)

          Survivorship proportional to fitness up to K: more realistic
              Selection affects recruitment to next generation
         Ex.: In AS system, deaths from malaria or sickle-cell are continuously "replaced"
                N continually "topped up" to K

            Darwin's Finch (Geospiza fortis) adapts to drought:
                larger birds survive because of changes in seed size & hardness

      Developmental canalization limits extent of directional selection
              Systems are controlled by multiple epistatic loci:
                    difficult to select on all loci simultaneously
              Organisms have developmental limits:
                   e.g. size cannot increase indefinitely
                  Johanssen bean experiment exhausted genetic variation within lineage
 

(2) Stabilizing Selection (AKA truncation selection)
      Fitness function has "peak"
          Variance reduced around constant trait mean at optimal phenotype,
              or tails of distribution eliminated (truncated)
 

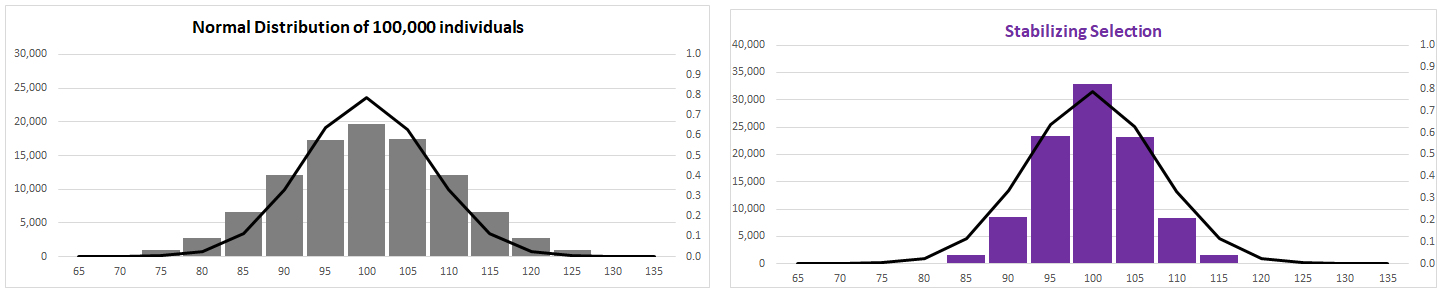
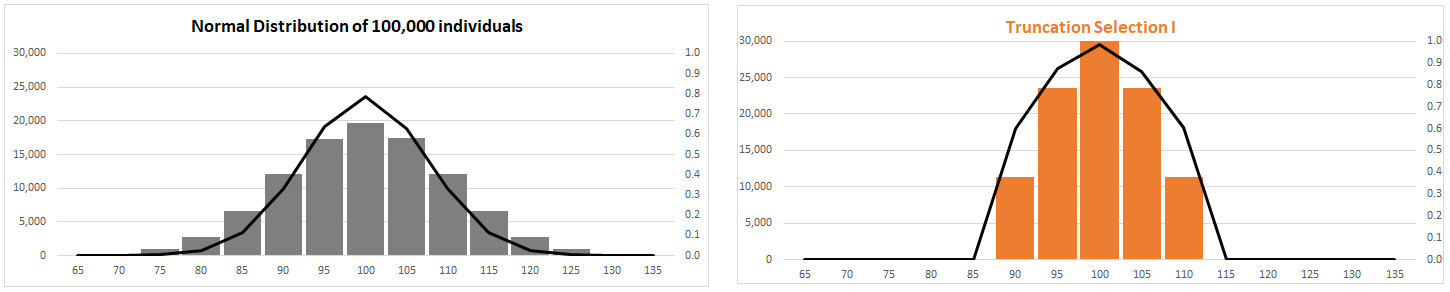
      Limits: elimination of  variant alleles
              or, 'weeding out' of disadvantageous variants
              homozygosity at multiple loci:
                    difficult iff variance due to recessive alleles
             inbreeding depression: loss of 'somatic vigor' in inbred lines

        Ex.:  Birth weight in Homo
                Modal birth weight has optimum survival
                Implications for future human evolution ?

(3) Diversifying Selection (two kinds)
      There is a lot of variation: can natural selection explain it?
       No single optimal from: trait variance increases

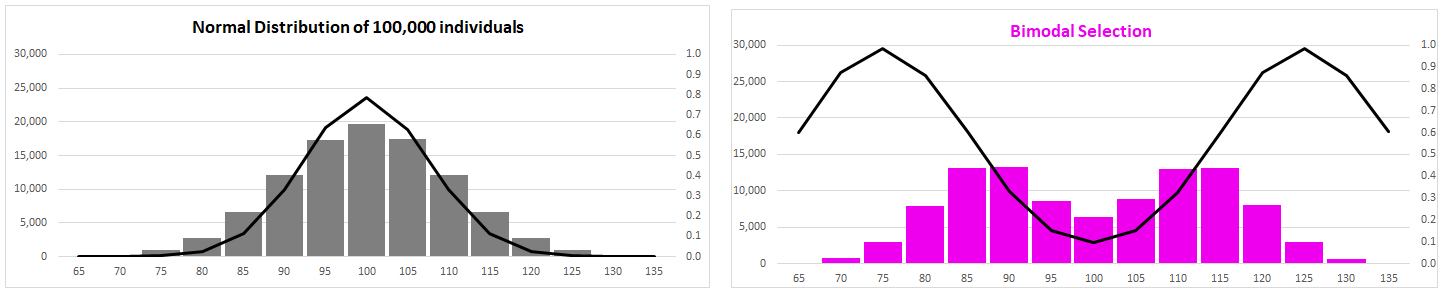
       polymorphic: variation maintained within populations
                Ex.: Genetic variation in corn snakes, tomatoes, bell peppers, snails
                Ex.: shell patterns in Cepaea snails
                       combinations of dark / light, banded / unbanded shells varies with substrate

       polytypic: variation distributed among populations
               Ex.: Clinal variation in Cepaea snails
                        patterns of banded / unbanded shells vary over short distances
              Müllerian mimicry:
                       Ex.: Heliconiusspp. butterflies exchange alleles by hybridization
                          Distasteful models converge on each other,
                          Different combinations evolve in different parts of range            

Text material © 2025 by Steven M. Carr