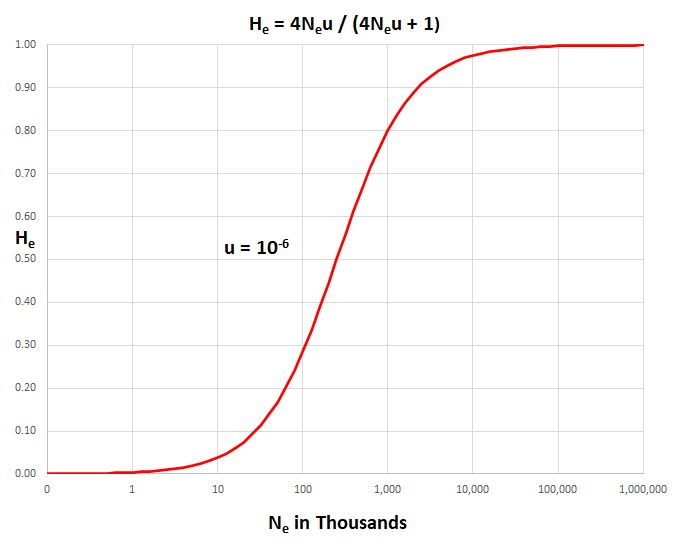
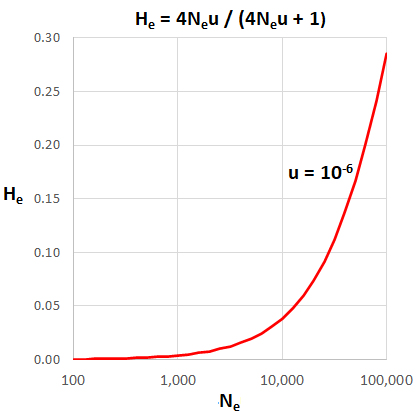
The Neutral Equation
According to the Neutral Theory, in the
absence of natural selection (s = 0), expected heterozygosity
(He) in a finite population of effective size Ne is a balance
between loss of variation by genetic drift
and its replacement by recurrent mutation at a
rate µ. Then it can be shown,
He = (4Neµ) / (4Neµ + 1)
If Ne = 106
and µ
= 10-6, then Neµ
= 1 and expected He
= (4)/(4 + 1) = 0.80. However, the observed range
0.001 < Hobs
< 0.25 over a wide range of species is much smaller than this expected value.
One interpretation is that the effective
population size (Ne) for most
species is much smaller than the observed
population count (Nc). Thus, if Ne = 104,
then Neu = 0.001 and He =
(0.004)/(0.004 + 1) = (0.004)/(1) = 0.04, a
fairly typical value.
A modified form is the Nearly-Neutral Theory where 0 ~
s << 1, which would allow larger populations
to have
lower He.



