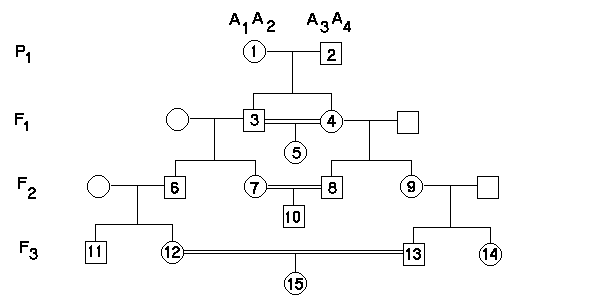
Consanguinity, Relatedness, & Inbreeding in pedigrees

Consanguineous matings (marriages, if humans are under discussion)
are those between related individuals, defined simply as
those that share a common ancestor. In pedigree charts, these
are indicated by double lines between symbols.
The Relatedness (r) of two consanguineous
individuals is the fraction of
alleles they share at all loci. This can be estimated
by analysis of any one locus. Any parent / offspring
combination must share exactly 1/2 of their
alleles at any locus: offspring inherit one or the other allele
from each of two parents: (1/2)(1/2) +
(1/2)(1/2) = 1/2. This is necessarily true for any single
locus. Any two full siblings are also expected
to share 1/2 of their alleles over all loci, but not
necessarily at any single locus. For example,
siblings #3 & #4 may each receive any of
four allele pairs from the parents: A1A3,
A1A4,
A2A3,
or A2A4.
There are thus 16 possible allelic relationships between
siblings at any one locus (see Table). In four of these,
both alleles are identical (r = 1), in
another four alleles all are distinct (r
= 0), and in eight only allele is shared (r
= 0.5). The expected r =
[(4)(1.0) + (4)(0.0) + (8)(0.5)] / (16) = 8/16 = 1/2.
For any finite sample of loci, measured r may deviate
from its expectation, the expected deviation being greater with
smaller samples.
| 1/3 |
1/4 |
2/3 |
2/4 |
|
| 1/3 |
1 |
0.5 |
0.5 |
0 |
| 1/4 |
0.5 |
1 |
0 |
0.5 |
| 2/3 |
0.5 |
0 |
1 |
0.5 |
| 2/4 |
0 |
0.5 |
0.5 |
1 |
For this reason,
estimates of genetic relatedness from commercial "DNA dot com"
DNA tests can be ambiguous. For example, 4th &
5th cousins have r = 1/64 and 1/128,
respectively, so that the expectation of allele sharing
across 512 tested loci is 8 vs 4,
respectively. Observed sharing of 3 ~ 9
alleles would not permit a statistical distinction to be be made
between these degrees of relationship. Estimation of relatedness
is further complicated when alleles are identical by state but
not by descent (see below). In the example
above, of the four alleles marked 1 2 3 & 4
in the P1, only two may be
distinguishable, such that both parents are A1A2.
Then, six of their
offspring will be genetically identical, eight related by 0.75,
and only two distinct [HOMEWORK:
show that this is true]. The sharing of these two alleles among
individuals in subsequent generations overestimates
relationship.
The offspring
of a consanguineous mating are described as inbred. The inbreeding coefficient (F) for an inbred individual is
the expectation that the individual has two alleles identical by descent (IBD) at any given locus. Alleles
are identical by descent if they are genetic copies of
the same allele in the common ancestor of the
consanguineous parents. These probabilities can be calculated by
following each allele through several generations. The concept
of IBD long antedates the discovery that genes are made
of DNA, however IBD occurs as the result of a
particular gene locus on a dsDNA molecule
replicating itself along two separate lineages.
For example, we
can calculate the probability that individual #5, the product of a full-sib mating,
has two alleles at the A locus that are identical by
descent as F = 1/4
= 0.25. Other relatedness and inbreeding
coefficients for typical consanguineous matings are shown below.
Consanguinity
and Inbreeding are
often confused. Because many humans exist and marry in more or
less closed, finite populations, any two marriage partners are
likely to have a more or less distant common ancestor, and are
therefore consanguineous distant cousins. Their
offspring would then be "inbred" and have
a calculable F. All finite populations are to some
degree "inbred," as measured by the average F
over all individuals in a population, and which is inversely
proportional to its size N. "Inbreeding"
becomes of special interest when the rate of marriages between
closely-related individuals is higher than expectation.
This may occur in societies where sib-sib
marriages are encouraged, as sometimes occurs for
religious reasons, or to keep property in the same family.
Western societies may discourage first-cousin marriages (but
Charles Darwin and his wife Emma Wedgwood were first cousins),
but attach no onus to marriages between second- or higher-degree
cousins. Most people may be unaware of fourth- or fifth-degree
cousins. (Recall that Queen Elizabeth II and HRH
Philip were fourth cousins).
HOMEWORK:
Show graphically
that individual #10, the product of a first-cousin
marriage, has F = 1/16.
Distinguish between consanguinity, relatedness,
and inbreeding. Give numerical examples.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|