Logic
of constructing a circular
restriction map
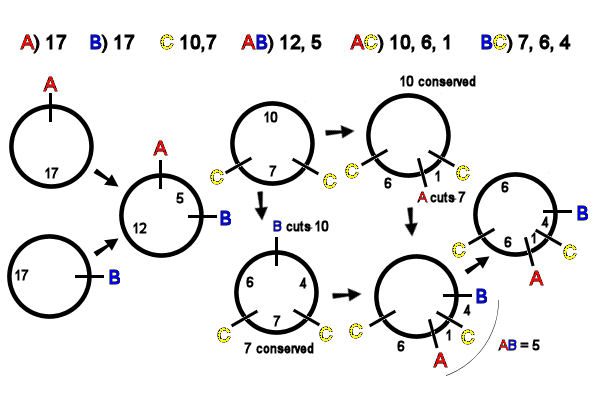
Digestion of a linear DNA molecule with
a restriction endonuclease (RE) that makes a single
cut produces two fragments. In contrast, digestion of a circular
DNA molecule with any RE that makes a single cut
produces a single linearized fragment, all of which
are necessarily of identical size. In the example, A & B each produce a linearized
circular molecule, length 17kb [far left]. Inspection of
the AB double digest data
shows that the A & B sites are 5kb
apart. The unique map of A
& B is thus easily
drawn [left, middle].
C cuts
the circle twice, producing two fragments: there
is only one possible map [middle, top]. Inspection of the AC double-digest data shows
that A cuts the (smaller)
7kb C
fragment. The unique map of A & C
is easily drawn [top, right] .
Inspection of the BC double-digest data [lower middle] shows that B cuts the (larger) 10kb
fragment of C.
There is only one way to diagram this, and the map of B & C is easily drawn [middle,
bottom] .
To integrate the AC and BC
maps, recall that AB
produces a 5kb fragment. Thus the B site is 5kb away
from A. If B were clockwise from A, B would cut the smaller C fragment into 1kb and 6 kb in
the BC diges], which the
data show is not so. If B is counter-clockwise from A, it would cut the larger C fragment into 4kb
and 6kb fragments,
which matches the data [right, bottom].
The final map of ABC places A
and B on either side of
the C site, and all
distances add up to 17kb, as expected [far right].
Circular restriction maps are important in
mapping plasmid DNA and mitochondrial DNA
molecules. The backbone of an mtDNA map is frequently the
placement of single-cut site REs, as above, A second clue
in mtDNA from vertebrate animals is the occurrence of two
Sst II sites at an interval of 1.6Kb
between two highly conserved regions of the larger and smaller rRNA
genes. These can serve to orient
the restriction map to the functional map of the
molecule.

