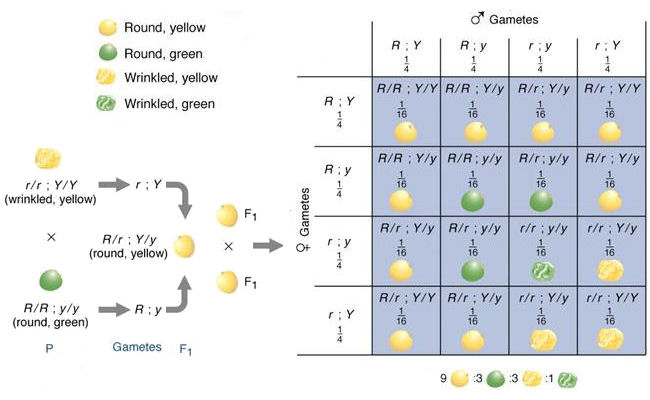
Mendel's explanation of the results of a dihybrid cross
Given
the
principles revealed in a monohybrid
cross, Mendel hypothesized that the result of two
characters segregating simultaneously (a dihybrid cross) would
be the product of their independent occurrence.
Consider two characters, seed color and seed shape. As
previously shown, Y
dominates y to
determine seed color, and R
factor for "round" dominates the r factor
for "wrinkled" to determine seed shape. He then proceeded
to test his hypothesis experimentally.
The P (Parental) cross is between true-breeding lines of wrinkled yellow peas (rrYY) and round green peas (RRyy). The F1 offspring are therefore all RrYy, and are all round and yellow. In forming the F2 plants, the alleles at the two loci segregate independently. That is, the chance of getting an R allele and a Y allele is 1/2 x 1/2, of getting an R and a y 1/2 x 1/2, and so on. Thus, all four possible diallelic combinations occur with an equal probability of 1/4. The same is true for both parents. Given four possible gamete types in each parent, there are 4 x 4 = 16 possible F2 combinations, and the probability of any particular dihybrid type is 1/4 x 1/4 = 1/16. The phenotypes and phenotypic ratios of these 16 genotype can be determined by inspection of the diagram above, called a Punnet Square after the geneticist who first used it.
Alternatively, recall that the phenotypic ratio expected for either character is 3:1, either 3 "Y" : 1 "y", or 3 "R" : 1 "R". Then, the expected phenotypic ratios of the two traits together can be calculated algebraically as a binomial distribution:
That is, we expect a characteristic 9:3:3:1 phenotypic ratio of round-yellow : wrinkled-yellow : round-green : wrinkled-green pea seeds.
To predict the genotypic ratios, recall that for each gene the ratio is 1 : 2 : 1 :: AA : Aa : aa . Then, algebraically
The P (Parental) cross is between true-breeding lines of wrinkled yellow peas (rrYY) and round green peas (RRyy). The F1 offspring are therefore all RrYy, and are all round and yellow. In forming the F2 plants, the alleles at the two loci segregate independently. That is, the chance of getting an R allele and a Y allele is 1/2 x 1/2, of getting an R and a y 1/2 x 1/2, and so on. Thus, all four possible diallelic combinations occur with an equal probability of 1/4. The same is true for both parents. Given four possible gamete types in each parent, there are 4 x 4 = 16 possible F2 combinations, and the probability of any particular dihybrid type is 1/4 x 1/4 = 1/16. The phenotypes and phenotypic ratios of these 16 genotype can be determined by inspection of the diagram above, called a Punnet Square after the geneticist who first used it.
Alternatively, recall that the phenotypic ratio expected for either character is 3:1, either 3 "Y" : 1 "y", or 3 "R" : 1 "R". Then, the expected phenotypic ratios of the two traits together can be calculated algebraically as a binomial distribution:
(3Y + 1y) x (3R + 1r) = 9YR + 3Yr + 3Ry + 1 ry
That is, we expect a characteristic 9:3:3:1 phenotypic ratio of round-yellow : wrinkled-yellow : round-green : wrinkled-green pea seeds.
To predict the genotypic ratios, recall that for each gene the ratio is 1 : 2 : 1 :: AA : Aa : aa . Then, algebraically
(1YY + 2Yy +
1yy) x (1RR +
2Rr + 1rr) = 1 YYRR + 2 YYRr + 1 YYrr + 2YyRR + 4YyRr +
2 Yyrr + 1yyRR + 2yyRr + 1yyrr
That is, we expect a
characteristic 1:2:1:2:4:2:1:2:1 ratio of the
nine possible genotypes. These nine genotypes can be
grouped into four phenotypes, for example 1 YYRR + 2 YYRr + 2 YyRR +
4 YyRr = 9Y-R- round, yellow peas. The ratio
of these phenotypes is of course 9:3:3:1.
Mendel reported the results of some but not all of the "7 choose 2" = (7)(7-1)/(2) = 21 possible dihybrid crosses with seven characters. He performed several trihybrid crosses as well.
Homework:
(1) Repeat the analysis above with a cross of RRYY x rryy.
(2) Predict the phenotypic and genotypic ratios of a trihybrid cross. Pea plants may be tall or short: use T for the tall allele, which is dominant to the t allele for short plants. How would you diagram such a cross?
(3) Suppose one character is semi-dominant (Aa intermediate between AA and aa). Predict the phenotypic and genotypic ratios in the offspring of a dihybrid cross between AaBb x AaBb where A is semidominant to a, and B is dominant to b.
Mendel reported the results of some but not all of the "7 choose 2" = (7)(7-1)/(2) = 21 possible dihybrid crosses with seven characters. He performed several trihybrid crosses as well.
Homework:
(1) Repeat the analysis above with a cross of RRYY x rryy.
(2) Predict the phenotypic and genotypic ratios of a trihybrid cross. Pea plants may be tall or short: use T for the tall allele, which is dominant to the t allele for short plants. How would you diagram such a cross?
(3) Suppose one character is semi-dominant (Aa intermediate between AA and aa). Predict the phenotypic and genotypic ratios in the offspring of a dihybrid cross between AaBb x AaBb where A is semidominant to a, and B is dominant to b.