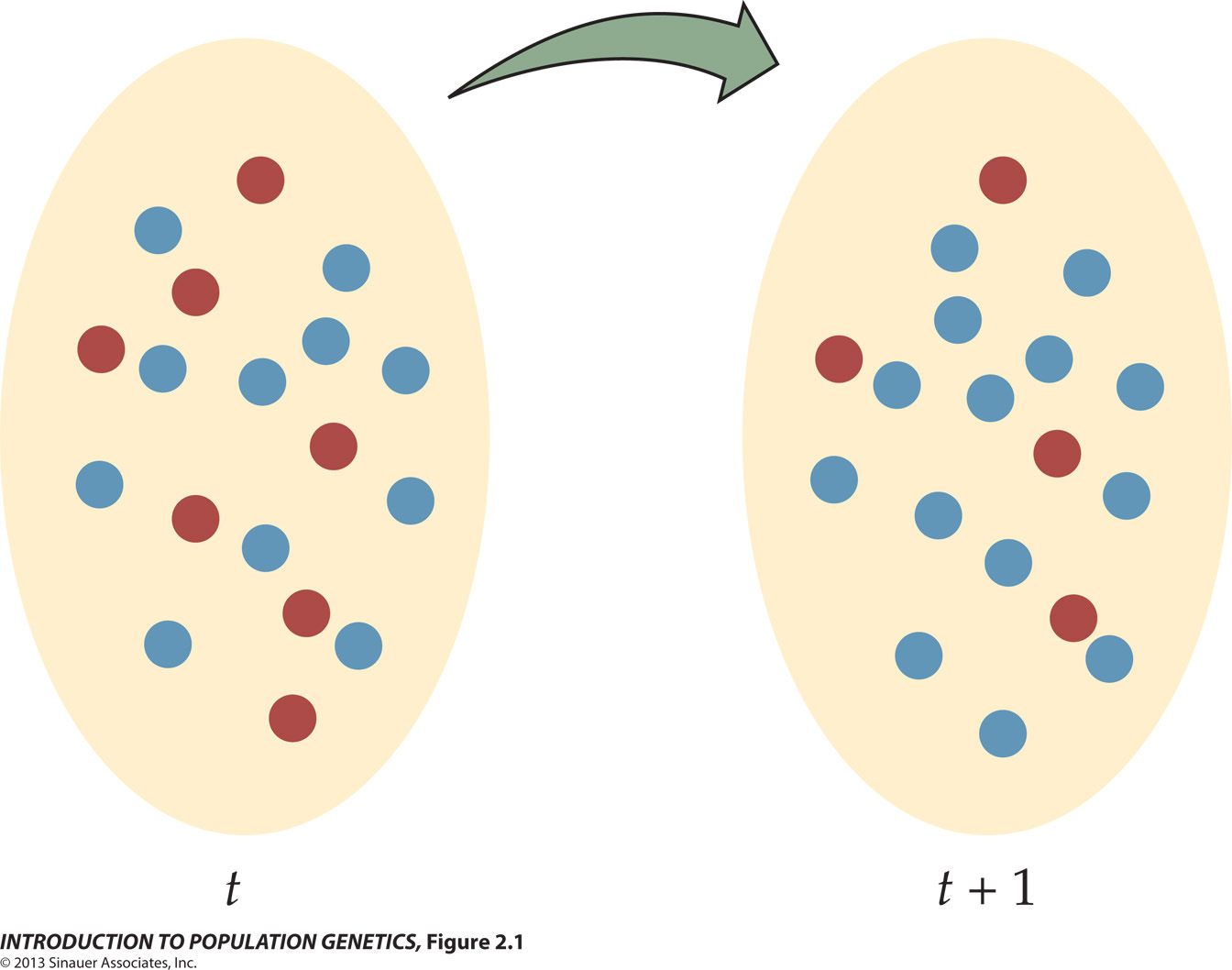
Two generations of the Wright - Fisher Model
Starting in generation t with 18
alleles for N =
18 haploid individuals, with f(A) = 7/18 = 0.39.
Generation t+1 comprises the same
number of alleles / individuals (18), but a modified f(A) = 4/18 =
0.22, due solely to random sampling error,
which Sewall Wright called genetic
drift.
The process of random sampling can be visualized as follows. Place 7 red and 11 blue marbles in a bag. Draw one at random: note its color. Return the marble to the bag. Repeat the process a total of 18 times. Create a new bag representing the next generation, containing 18 marbles in the proportions obtained by the random draw.
The Wright - Fisher Model considers haploid individuals, but can be adjusted for diploid populations. Here, the 18 haploid individuals can be treated as nine diploid individuals with two alleles each. This is equivalent to the 'tide pool' model used to derive the Hardy-Weinberg Theorem for random union of gametes. As a diploid model, it is slightly unrealistic in that it ignores genotypic, two-allele combinations, and allows self-fertilization (if the same marble were drawn twice in a row).
The process of random sampling can be visualized as follows. Place 7 red and 11 blue marbles in a bag. Draw one at random: note its color. Return the marble to the bag. Repeat the process a total of 18 times. Create a new bag representing the next generation, containing 18 marbles in the proportions obtained by the random draw.
The Wright - Fisher Model considers haploid individuals, but can be adjusted for diploid populations. Here, the 18 haploid individuals can be treated as nine diploid individuals with two alleles each. This is equivalent to the 'tide pool' model used to derive the Hardy-Weinberg Theorem for random union of gametes. As a diploid model, it is slightly unrealistic in that it ignores genotypic, two-allele combinations, and allows self-fertilization (if the same marble were drawn twice in a row).