A stable equilibrium
 (where
(where 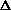 q
= 0) is reached
q
= 0) is reached
when the rate of replacement (by mutation)
balances the rate of removal (by selection).
Deleterious
alleles are maintained by recurrent mutation.
A stable
equilibrium (where
(where 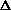 q
= 0) is reached
q
= 0) is reached
when the rate of replacement (by mutation)
balances the rate of removal (by selection).
µ
=
frequency of new mutant alleles per locus per generation
typical µ =
10-6: 1 in 1,000,000 gametes has
new
mutant
_____
then  =
=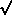 (µ
/ s) [see derivation]
(µ
/ s) [see derivation]
Ex.: For a recessive lethal allele (s = 1) with a
mutation
rate of µ = 10-6
then 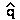 = û
=
= û
= 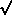 (10-6
/ 1.0) = 0.001
(10-6
/ 1.0) = 0.001
mutational
genetic
load
Lowering selection against alleles increases their frequency.
Medical intervention has increased the frequency of heritable
conditions
in Homo (e.g., diabetes, myopia)
Eugenics:
modification of human condition by selective breeding
'positive eugenics': encouraging people with "good genes" to
breed
'negative eugenics': discouraging people with 'bad genes'' from
breeding
e.g., immigration control, compulsory sterilization
[See: S. J. Gould, "The
Mismeasure of Man"]
Is
eugenics effective at reducing frequency of deleterious alleles?
What proportion of 'deleterious alleles' are found in heterozygous
carriers?
(2pq)
/ 2q2 = p/q 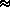 1/q
(if q << 1)
1/q
(if q << 1)
if s = 1 as above, ratio is 1000 / 1 : most of
variation
is in heterozygotes,
not subject to selection
Directional
selection is balanced by influx of 'immigrant' alleles;
a stable 'equilibrium' can be reached iff migration rate constant.
Consider an island adjacent to a
mainland,
with unidirectional
migration to the island.
The fitness values of the AA, AB,
and BB genotypes differ in the two environments,
so that
the allele frequencies differ between the mainland (qm)
and the island (qi).
| AA | AB | BB | ||
|
|
W0 | W1 | W2 | q |
| Island | 1 | 1-t | 1-2t | qi |
| Mainland | 0 | 0 | 1 | qm |
B has high fitness on
mainland,
and low fitness on island.
[For this model only,
allele A is semi-dominant to allele B,
so we use t for the selection coefficient to avoid confusion]
m
=
freq. of new migrants (with qm)
as fraction of residents (with qi)
if m
<< t qi
= (m / t)(qm)
[see derivation]
Gene flow can hinder optimal adaptation of a population to local conditions.
Ex: Water
snakes (Natrix sipedon) live on islands
in Lake Erie (Camin & Ehrlich 1958)
Island
Natrix mostly unbanded; on adjacent mainland, all
banded.
Banded snakes are non-cryptic on limestone islands, eaten by gulls
Suppose A = unbanded B
= banded [AB are intermediate]
Let qm =
1.0
["B" allele is fixed on mainland]
m = 0.05 [5% of island snakes are new
migrants]
t = 0.5 so W2
= 0 ["Banded" trait is lethal on island]
then qi =
(0.05/0.5)(1)
= 0.05
and Hexp = 2pq =
(2)(0.95)(0.05) 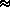 10%
10%
i.e, about 10% of snakes show intermediate banding, despite
strong
selection
=> Recurrent migration can maintain a disadvantageous trait at high
frequency.
Inbreeding
is the mating of (close) relatives
or, mating of individuals with at least one common ancestor
F (Inbreeding
Coefficient) = prob. of "identity
by descent":
Expectation that two alleles
in an individual are
exact genetic copies of an allele in
the
common ancestor
or, proportion of population with two
alleles identical by descent
This is determined by the consanguinity (relatedness) of parents.
Inbreeding
reduces
Hexp by a proportion F
(& increases the proportion of homozygotes). [see
derivation]
f(AB) = 2pq (1-F)
f(BB) = q2 + Fpq
f(AA) = p2 + Fpq
Inbreeding
affects genotype proportions,
inbreeding does not affect allele frequencies.
Inbreeding
increases the frequency of individuals
with deleterious recessive genetic diseases by F/q [see derivation]
Ex.: if q = 10-3 and F
= 0.10 , F/q = 100
=> 100-fold increase in f(BB) births
Inbreeding coefficient of a population can be estimated from experimental data:
F = ( 2pq - Hobs ) / 2pq [see derivation]
Ex.: Selander (1970) studied structure of Mus house mice living in chicken sheds in Texas|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& q = 0.374 + (1/2)(0.400) = 0.574
Then F = (0.489 - 0.400) /
(0.489)
= 0.182
which is
intermediate
between Ffull-sib =
0.250
& F1st-cousin = 0.125
=> Mice live
in small
family groups with close inbreeding
[This is typical for small mammals]
However, in combination with natural selection, inbreeding can be
"advantageous":
increases rate of evolution in the long-term (q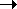 0 more quickly)
0 more quickly)
deleterious alleles are eliminated more quickly.
increases phenotypic variance (homozygotes are more
common).
advantageous alleles are also reinforced in homozygous form
Genetic
Drift is stochastic 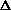 q
[unpredictable,
random]
q
[unpredictable,
random]
(cf. deterministic 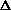 q
[predictable,
due to selection, mutation, migration)
q
[predictable,
due to selection, mutation, migration)
Sewall Wright (1889 - 1989): "Evolution and the Genetics of Populations"
Stochastic 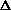 q
> deterministic
q
> deterministic 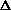 q
in small populations:
q
in small populations:
allele frequencies drift more rapidly in 'small' than 'large'
populations.
Drift is
most noticeable if s 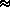 0,
and/or N small (< 10) [N
0,
and/or N small (< 10) [N 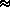 1/s]
1/s]
genetic variance
= 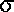 q2 = (q)(1
- q) / 2N
q2 = (q)(1
- q) / 2N
if q = p = 0.5, then 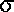 q2 =
1 / 8N
q2 =
1 / 8N
q
drifts among populations (among population
variance
increases);
eventually, half lose the allele, half fix it.
Ex:
[Demonstration
#3]
[Try: q = 0.5, W0 = W1 = W2 = 1.0, and N = 10, 50, 200, 1000;
repeat 10 trials each, note q at
endpoint]
**=> Variation is 'fixed' or 'lost' & populations will diverge by chance <=**
Evolutionary
significance:
"Gambler's Dilemma" : if you play
long enough, you win or lose
everything.
All populations are finite: many are very small,
somewhere
or sometime.
Evolution occurs on vast time scales: "one in a million chance"
is a certainty.
Reproductive success of individuals in variable: "The race
is
not to the swift ..."
What happens in the really long run?
Effective
Population Size (Ne)
= size of an 'ideal'
population with same genetic variation (measured
as
H)
as the observed 'real' population.
= The 'real' population
behaves evolutionarily like one of size Ne
:
e.g., the population will
drift like one of size Ne
loosely,
the
number of breeding individuals in the population
Consider three special cases where Ne < or << Nobs [the 'count' of individuals]:
(1) Unequal sex ratio
Ne = (4)(Nm)(Nf) /
(Nm + Nf)
where Nm & Nf are numbers of breeding males & females, respectively.
"harem" structures in mammals (Nm << Nf)
Ex.: if Nm = 1 "alpha male" and Nf
= 200
then Ne = (4)(1)(200)/(1 +
200) 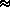 4
4
A single male elephant
seal (Mirounga)
does most of the breeding
Elephant seals have very low genetic variation
eusocial (colonial)
insects
like ant & bees (Nf << Nm)
Ex.: if Nf = 1 "queen" and Nm=
1,000 drones
then Ne = (4)(1)(1,000)/(1 +
1,000) 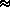 4
4
Hives are like single small families
(2) Unequal
reproductive success
In stable population, Noffspring/parent
= 1
"Random" reproduction follows
Poisson
distribution
(N = 1 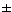 1)
1)
(some parents have 0, most
have 1, some have 2, a few have 3 or more)
| X | 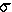 |
Ne = | Reproductive strategy |
| 1 | 1 | Nobs | Breeding success is random |
| 1 | 0 | 2 x Nobs | A zoo-breeding strategy |
| 1 | >1 | < Nobs | K-strategy, as in Homo |
| 1 | >>1 | << Nobs | r-strategy, as in Gadus |
(3) Population size variation over time
Ne = harmonic mean
of N = inverse of arithmetic mean of inverses
[a harmonic mean is much closer to lowest value in series]
n
Ne = n / [  (1/Ni)
] where Ni = pop size in
i th
generation
(1/Ni)
] where Ni = pop size in
i th
generation
i=1
Populations
exist in changing environments:
Populations are unlikely to be stable over very long periods of time
10-2 forest fire / 10-3 flood / 10-4
ice
age
Ex.: if typical N = 1,000,000 & every 100th
generation
N
= 10 :
then Ne = (100) / [(99)(10-6) +
(1)(1/10)] 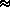 100 / 0.1 = 1,000
100 / 0.1 = 1,000
Founder
Effect & Bottlenecks:
Populations are started by (very) small number of individuals (N=2),
or undergo dramatic reduction in size (N
< 10)).
Ex.: Origin of Newfoundland moose (Alces):
2 bulls + 2 cows at Howley in 1904
[maximum 8 alleles / locus, likely less if
single source population]
[1 bull + 1 cow at Gander in 1878 didn't succeed].
Population
cycles: Hudson
Bay Co. trapping
records (Elton 1925)
Population densities of lynx, hare, muskrat cycle over several orders
of
magnitude
Lynx cycle appears to "chase" hare cycle
The effect of drift on genetic variation in populations
Larger populations are more variable (higher H) than
smaller
if s = 0: H
reflects balance between loss of
alleles
by drift
and replacement by mutation
H = (4Neµ) / (4Neµ + 1) [the "neutralist equation"]
Ex.: if µ= 10-7 & Ne = 106 then Neµ = 1 and Hexp = (0.4)/(0.4 + 1) = 0.29
But
typical
Hobs 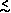 0.20 which suggests Ne
0.20 which suggests Ne 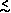 105
105
Most natural populations have a much
smaller
effective size than their typically observed size.
Ex.: Gadus
morhua in W. Atlantic were
confined to Flemish
Cap during last Ice
Age 8~10 KYBP
mtDNA sequence variation occurs as "star
phylogeny":
most variants are rare and related to a common surviving genotype
Carr et al. 1995 estimated
Ne = 3x104
as compared with Nob s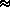 109
109
Effective size is ca. 5 orders of magnitude smaller than
observed
Marshall
et al. (2004) showed that "genome-types" at
Flemish Cap are distinctive
Stochastic effects may be as or more important than deterministic
processes
in long-term evolution.