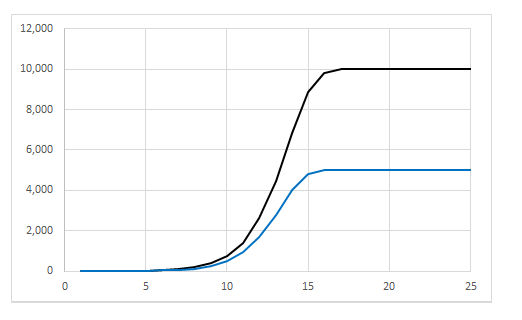
Logistic growth
A key insight of Darwin
in formulating his Theory of Natural Selection was the
recognition that, as Malthus had argued, all species'
numbers tend to increase geometrically, whereas resources
increase arithmetically at best. In terms of modern
ecological theory, in the absence of checks to natural increase,
population size N would increase geometrically over time at some intrinsic
growth rate r, so that
dN/dt = rN. [Then, r is the compound
interest rate on N].
If the environment imposes a upper limit K (carrying
capacity) to population size, N increases
by a logistic growth
curve towards K, such that the limit to dN/dt
=
rN (K-N) / K : the rate of growth slows as N approaches
K. Carrying capacity of the environment may be a
consequence of biotic and (or) abiotic factors,
for example the presence of prey and predators or the amount of
rainfall and rocky habitat. When N << K, the
exponential and logistic expectations for N are about
equal.
In the example above, r = 2 such that
the population tends to double every generation, and K =
10,000. The black curve shows the population size N
at any point, and the blue curve
shows 
N
as
the discrete value of dN/dt , the
change in N per generation