Derivation of the General Selection Equation

---

______________________________________________________________

Genotype         AA                  AB                BB
______________________________________________________________

(1) Frequency     p²            +    2pq            +    q²             =               1
before selection

(2)  Fitness         W₀                  W₁                 W₂

(3) Relative        p²W₀        +    2pqW₁       +    q²W₂        =              
Contribution

(4) Frequency    p²W₀/  +   2pqW₁/  +    q²W₂/  = / = 1
after selection
 ______________________________________________________________

(1) Genotype distributions before selection follow Hardy-Weinberg expectations.

(2) Each genotype AA, AB, and BB has a distinct phenotype: W₀, W₁, & W₂, respectively.
    W is the expectation that an individual with a particular genotype will survive & reproduce

(3) Each genotypic class makes a relative contribution to the next generation,
        which is proportional to its initial frequency, weighted by its fitness.

    [e.g., if the AA genotype has a frequency of 0.25 and 80% survive to reproduce,
             the relative contribution of AA to the next generation is (0.25)(0.8)=0.20]
    
    The sum of the relative contributions of all three genotypes is 
       (read as, "W bar") = mean population fitness
        In this simple model,< 1, because not everyone on Line (1) survives.

(4) Because  < 1, the relative contributions have to be "normalized":
    Dividing the contribution of each genotype by returns the sum to unity,
    and the final values are the relative genotype frequencies after selection.

---

To derive the allele frequencies after selection, take Line (4) above and

recall  q = f(BB) + (1/2) f(AB)

    so  q' =  q²W₂/  + (1/2) 2pqW₁/   =  q(qW₂ + pW₁)/ 

then 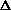 q   =  q' - q  = q_after - q_before

                =  q(qW₂ + pW₁)/  -  q/ 

                =  [(q)(qW₂ + pW₁) - (q)(p²W₀ + 2pqW₁ + q²W₂)] / 

                =  [(q)(qW₂ + pW₁ - p²W₀ - 2pqW₁ - q²W₂)] / 

                =  [(q)(pqW₂ + W₁p(1-2q) - pW₀p)] /                     [Note 1]

                =  [(pq)(qW₂ + W₁(1-2q) - W₀p)] / 

                =  [(pq)(W₂q + W₁(p-q) - W₀p)] /                          [Note 2]

                =  [(pq)(W₂q + W₁p - W₁q - W₀p)/ 

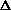            q  =  [pq] [(q)(W₂ - W₁) + (p)(W₁ - W₀)] / []
________________________________________________

Notes: [1]  (q - q²) = q(1 - q) = pq        [2]  (1 - 2q) = (1 - q) - q = p - q

---

Homework:  repeat this derivation for 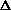  p = p' - p

---

Text material © 2022 by Steven M. Carr

---