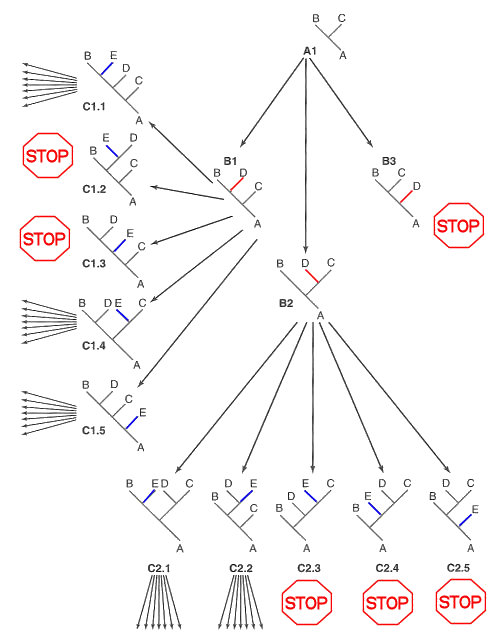
Branch & Bound Method of Network Search
For three
terminal taxa, A, B, & C, only one network
is possible (A1). A
fourth taxon D can be
added as a new branch on any of the three existing branches,
to create three networks B1, B2,
& B3. Each has four
branches and one internode.
Inspection of B1 establishes an upper bound for the four-taxon
network: calculation for the other two shows that B2 has the same length, but
B3 exceeds this bound.
Therefore B3 network and
all derivative networks can be excluded from further
examination. A fifth taxon E can now be added on any of the four branches
or the internode of remaining two networks B1 and B2, creating ten
networks for evaluation. Inspection of network C1.1 establishes a new upper
bound: calculation shows that two of the five C1 and
three of the C2 trees exceed this limit, which
are then eliminated from further consideration. This "Branch
& Bound" search algorithm continues with the addition
of a sixth taxon F to
any of the five branches and two internodes in the five
remaining networks, establishment of a new upper bound, and so
on.
Notice that the first step eliminated one-third of the possible networks, and the second step one-half of the remaining possibilities, so that by the third step it is only necessary to evaluate one-sixth of the original possible "network space." Under favorable circumstances, only one network remains at each step, and the single shortest tree is quickly identified. Branch & Bound is a computationally efficient algorithm that is guaranteed to find the shortest network(s) for analyses of up to ~20 taxa, for which there are 8.2 x 1027 possible rooted networks (trees). Beyond this, because the number of possible networks continues to increase hyper-exponentially, the algorithm requires too much computer time to be practical.
Notes on Tree computation & Storage: At each successive step in this process, when a minimum-length network is identified, its topology & branch lengths need to be stored if the solution is to be displayed. Thus the machine storage space allocated to this also increases hyper-exponentially, which may be more limiting than CPU time per se. As a simple computational problem, an alternative solution is to keep track of only the length of the shortest tree at any step, and to report this number at the end of the search. This requires the same machine time but far less machine storage than the first approach. It may then be possible to generate networks at random, automatically rejecting any that exceed the already-determined minimum length. Other strategies are possible.
Carr, Marshall, Wareham, & Craig (2015) discuss different strategies of biological computation, as applied to algorithmic, computational, & approximation approaches to identification of Open Reading Frames in DNA.
Notice that the first step eliminated one-third of the possible networks, and the second step one-half of the remaining possibilities, so that by the third step it is only necessary to evaluate one-sixth of the original possible "network space." Under favorable circumstances, only one network remains at each step, and the single shortest tree is quickly identified. Branch & Bound is a computationally efficient algorithm that is guaranteed to find the shortest network(s) for analyses of up to ~20 taxa, for which there are 8.2 x 1027 possible rooted networks (trees). Beyond this, because the number of possible networks continues to increase hyper-exponentially, the algorithm requires too much computer time to be practical.
Notes on Tree computation & Storage: At each successive step in this process, when a minimum-length network is identified, its topology & branch lengths need to be stored if the solution is to be displayed. Thus the machine storage space allocated to this also increases hyper-exponentially, which may be more limiting than CPU time per se. As a simple computational problem, an alternative solution is to keep track of only the length of the shortest tree at any step, and to report this number at the end of the search. This requires the same machine time but far less machine storage than the first approach. It may then be possible to generate networks at random, automatically rejecting any that exceed the already-determined minimum length. Other strategies are possible.
Carr, Marshall, Wareham, & Craig (2015) discuss different strategies of biological computation, as applied to algorithmic, computational, & approximation approaches to identification of Open Reading Frames in DNA.