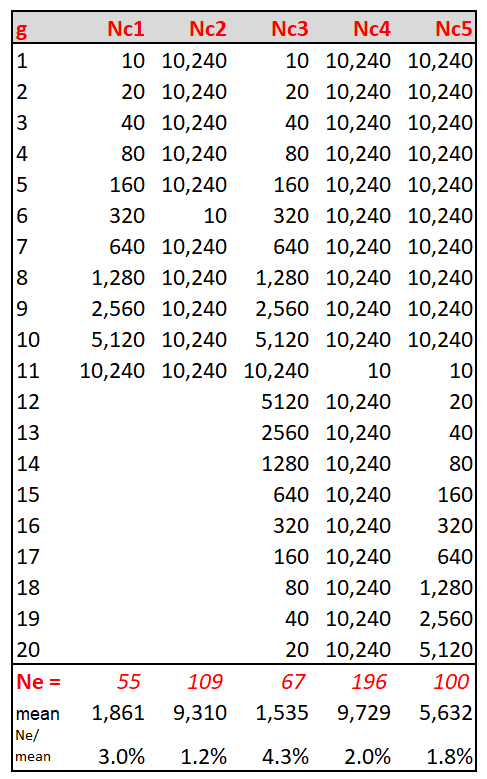
Effect on Ne of variable population size (Nc) over time:
Five scenarios
In a population that is
variable over time, Ne is the harmonic mean of the number
of breeding individuals in each generation. The harmonic
mean of a series is defined as the inverse of the
mean of inverses, and is dominated by the smaller
numbers in the series.
Consider five scenarios for the change in census count (Nc) over time (Nc1 - Nc5). (1) A founding population of 10 individuals that doubles every generation up to 10,000 individuals behaves like a population of N = 55. (2 & 4) Populations that typically comprises 10,000 individuals, but once in 10 (Nc2) or 20 (Nc4) generations undergo a bottleneck to 10, behave like populations ~1/100 or ~1/50 the typical size, respectively. These extreme events may not be evident in populations not subject to long-term study. (3) A population that cycles between 10 and 10,000 individuals by doubling to the peak and then halving to the trough, and repeating, has an even smaller Ne than a population subject to a single bottleneck. (5) A population that after drastic reduction rebuilds slowly (Ro = 2) to its former size has about one-half the Ne of a population that recovers quickly (Nc4)
Homework: Assume bottlenecks as in scenarios Nc2 & Nc4, where a drastic reduction from 10,000 to 100 occurs once every 100th generation. Estimate Ne. [Hint: The question asks for an estimate, not an exact calculation. What is the numerical relation to scenarios 2 & 4 ?]
Consider five scenarios for the change in census count (Nc) over time (Nc1 - Nc5). (1) A founding population of 10 individuals that doubles every generation up to 10,000 individuals behaves like a population of N = 55. (2 & 4) Populations that typically comprises 10,000 individuals, but once in 10 (Nc2) or 20 (Nc4) generations undergo a bottleneck to 10, behave like populations ~1/100 or ~1/50 the typical size, respectively. These extreme events may not be evident in populations not subject to long-term study. (3) A population that cycles between 10 and 10,000 individuals by doubling to the peak and then halving to the trough, and repeating, has an even smaller Ne than a population subject to a single bottleneck. (5) A population that after drastic reduction rebuilds slowly (Ro = 2) to its former size has about one-half the Ne of a population that recovers quickly (Nc4)
Homework: Assume bottlenecks as in scenarios Nc2 & Nc4, where a drastic reduction from 10,000 to 100 occurs once every 100th generation. Estimate Ne. [Hint: The question asks for an estimate, not an exact calculation. What is the numerical relation to scenarios 2 & 4 ?]
Figure & Text material © 2024 by Steven M. Carr