The Poisson distribution is a special case of the binomial distribution that applies where the phenomenon under study occurs as rare, discrete events (count data). The characteristic statistical property of a Poisson distribution is that the variance equals the mean (σ² = µ). For a Poisson-distributed process, the probability P of observing Y events given a mean = u is

P(Y,u) = e^-u u^Y / Y!

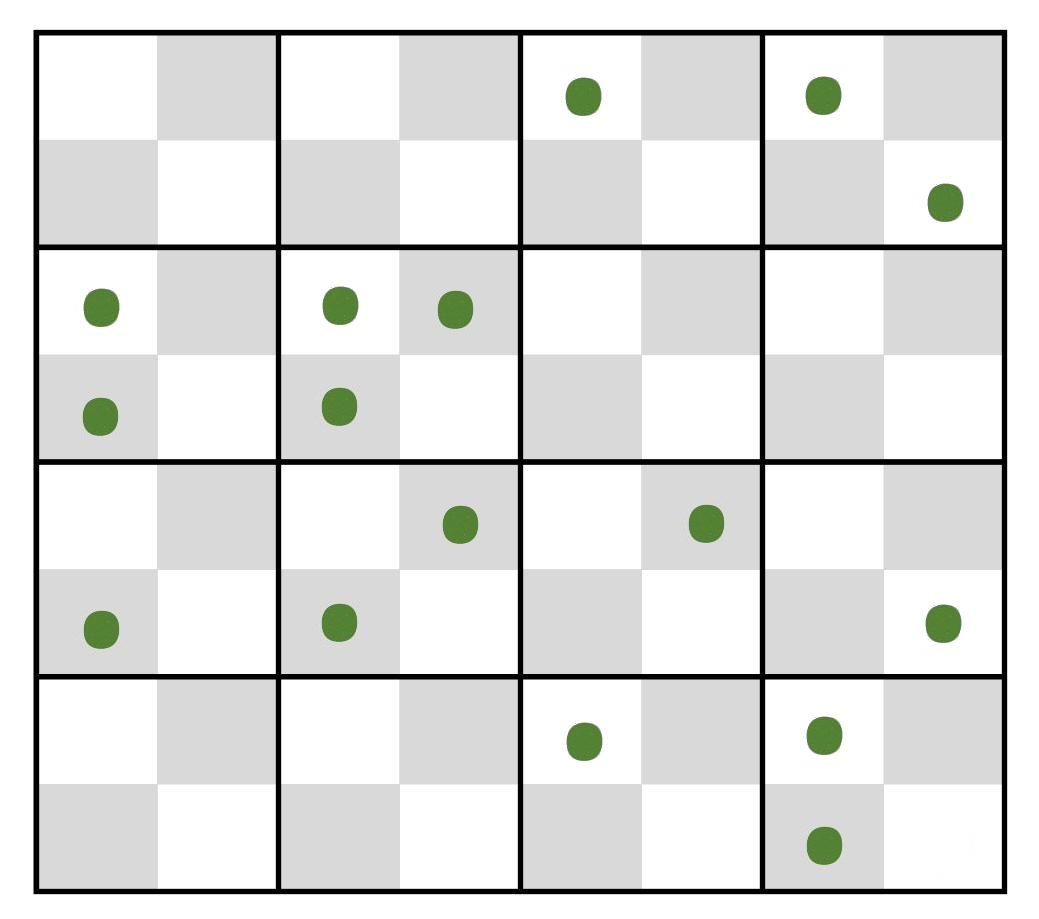
   (1) In an ecological study of the distribution of a rare plant species among a number of standardized quadrat plots, a majority of plots may be expected to contain no plants, a smaller number a single plant, and still smaller numbers two, three, or more plants. If 16 plants are distributed randomly over the 4 x 4 checkerboard of 2 m² quadrats [heavy outlines] below (mean µ = 1), the table shows that a random Poisson distribution over the cells should produce "0" and "1" classes at 37% each, a "2" class at 18%, the "3" class at 6%, and the more frequent classes will take up the remaining 2%. In the example, the 16 plants are distributed over 6, 5, 4, and 1 cells with 0, 1, 2, and 3 plants, respectively. A Chi-square test based on an expected µ = 1 ± 1 distribution would indicate whether or not the rare plant species is distributed randomly.

4X4 quadrat with 16 plants

    (2) The Poisson can simplify analysis of a simple "either / or" data set. In the quadrat example with µ = 1, the Poisson random expectation is that 37% of the quadrat plots will be unoccupied (0) and the remaining 63% occupied (> 0). In the example, there are 6 unoccupied cells and 10 occupied cells in the 4 x 4 quadrat. In a 2x2 contingency test (for example, Fisher's Exact Test), a significant excess of empty cells means the plants are clumped, and a significant deficiency means the plant distribution is more uniform. The former might occur if suitable soil is patchily distributed, the latter if successful plants are spaced out so as to avoid competition for resources.

    (3) The same principle can be extended to a multiple hits correction. For example, if I throw rocks at a building with 100 windows, a good early estimate of the number of thrown rocks is the count of broken windows. After a bit, this count is an underestimate, because once a window is broken, any subsequent rock that goes through the same space is not counted. We can then apply a Poisson Correction to estimate the number of multiple hits from the zero class (the number of unbroken windows). From the above, the expected probability of the zero class (P0) simplifies to

      P₀ = e^-u u⁰ / 0! = e^-u

     where u = corrected fraction of hits. For example, if 39 out of 100 windows are broken, then 61 are unbroken (P₀ = 0.61), so set 0.61 = e^-u
 
     Taking the negative natural log of both sides gives u = - ln(0.61) = 0.50

    That is, the estimated number of "hits" is (100)(0.50) = 50 rather than the observed 39 broken windows, that is, 11 extra "hits". This requires a correction of (50 - 39) / 39 = (11 / 39) = 28%. From the table above, note that the correction of 11 extra events correspond roughly to 8 windows with "double" hits and 1 with "triple" hits, total (8)(1) + (1(2) = 10.

    The Poisson Correction is extremely valuable in molecular population genetics, where it can be used to correct the number of actual nucleotide and (or) amino acid differences from the number observed between two macromolecules

 (4)  In a classic study, Bortkiewicz (1898) studied the distribution of 122 soldiers kicked to death by horses among ten Prussian army corps over 20 years. The data show that, in most years in most corps nobody dies from horse kicks, whereas in one corp in one year, four men were kicked to death. Do the data suggest that members of this particular corp were careless?  Statistical analysis indicates that the observed frequencies conform quite closely to the expected Poisson frequencies: the mean and variance are identical.  The corp was "unlucky" rather than careless: it fell in the extreme tail of the expected distribution of events.

Number of men kicked to death by horses in ten Prussian army corps