Introduction to Game Theory (II)
Given a 2x2 game
without a saddle-point, an optimal Mixed Strategy
for each player can be calculated. The generalized
solution of M x N games requires Matrix
Algebra: for 2x2 games the solution can be
calculated arithmetically.
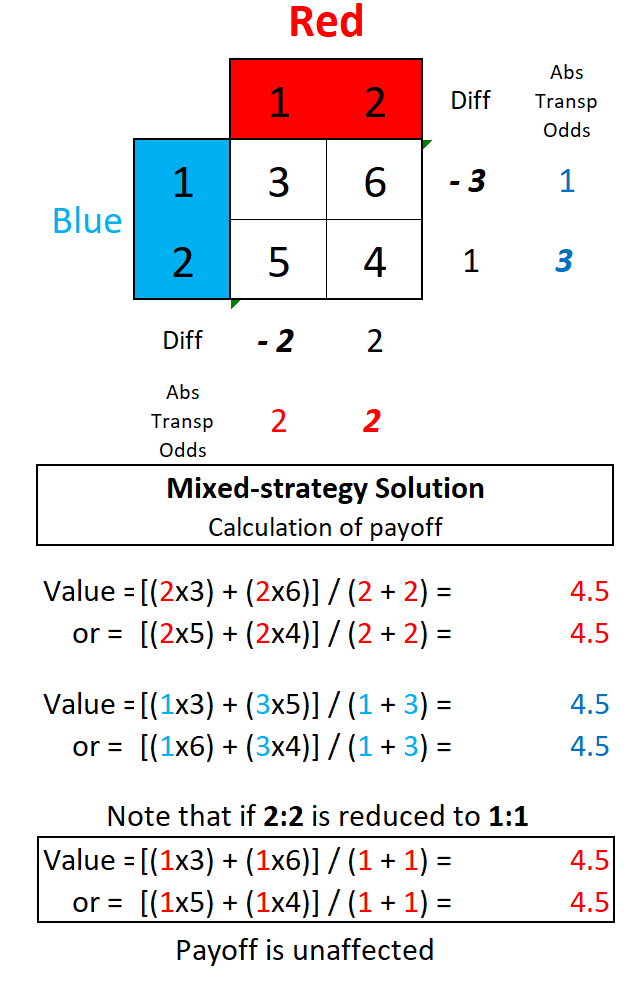
For each Blue row, subtract Red Strategy 2 from Red Strategy 1, then transpose the absolute differences of the rows. The procedure for Red is the same, but calculated from column differences. These marginal values (oddments) give the optimal ratio of strategies (to be mixed at random) for Blue to maximize the Value of the game, and for Red to minimize the loss. This Value is calculated as the sum of the oddment for any row times the payoff for each cell, all divided by the sum of the ratios (oddments). As shown for Row 1, this is [(1 x 3) + (3 x 5)] / (1 + 3) = 4.5. The same result should be obtained from any column or row in the matrix. This algorithm can be applied to games of greater interest.
Any departure by either player from the optimal mix of strategies will lower the value of the game to that player, so long as the other player continues to use their optimal strategy. The game as presented is a "zero-sum game", with "losses" plus "gains" equal to zero. This game is "unfair" to Red, as the mean payoff per game to Blue is 4.5. The game can be made "fair" by subtracting 4.5 from each element of the payoff matrix, or by having Blue make a side-payment of 4.5 to Red for each play of the game. The 2:2 ratio for Red is reducible to 1:1, without changing the payoff of the game. Matrix algebra is commutative: adding to or multiplying each cell value by a constant increases the payoff by the amount added or multiplied, but does not changed the mixed strategy oddments.
For each Blue row, subtract Red Strategy 2 from Red Strategy 1, then transpose the absolute differences of the rows. The procedure for Red is the same, but calculated from column differences. These marginal values (oddments) give the optimal ratio of strategies (to be mixed at random) for Blue to maximize the Value of the game, and for Red to minimize the loss. This Value is calculated as the sum of the oddment for any row times the payoff for each cell, all divided by the sum of the ratios (oddments). As shown for Row 1, this is [(1 x 3) + (3 x 5)] / (1 + 3) = 4.5. The same result should be obtained from any column or row in the matrix. This algorithm can be applied to games of greater interest.
Any departure by either player from the optimal mix of strategies will lower the value of the game to that player, so long as the other player continues to use their optimal strategy. The game as presented is a "zero-sum game", with "losses" plus "gains" equal to zero. This game is "unfair" to Red, as the mean payoff per game to Blue is 4.5. The game can be made "fair" by subtracting 4.5 from each element of the payoff matrix, or by having Blue make a side-payment of 4.5 to Red for each play of the game. The 2:2 ratio for Red is reducible to 1:1, without changing the payoff of the game. Matrix algebra is commutative: adding to or multiplying each cell value by a constant increases the payoff by the amount added or multiplied, but does not changed the mixed strategy oddments.
Example from JD Williams (1966); Figure & Text material © 2024 by Steven M. Carr