General Selection Model

Derivation of the General Selection Equation
______________________________________________________________

Genotype         AA                  AB                BB
______________________________________________________________

(1) Frequency     p²            +    2pq            +    q²             =               1
before selection

(2) Fitness         W₀                  W₁                 W₂(3) Relative        p²W₀        +    2pqW₁       +    q²W₂        =

Contribution

(4) Frequency p²W₀/

+ 2pqW₁/

+ q²W₂/

= 1
after selection
______________________________________________________________

(1) Genotype distributions before selection follow Hardy-Weinberg expectations.

(2) Each genotype AA, AB, and BB has a distinct phenotype: W₀, W₁, & W₂, respectively.
    W is the expectation that an individual with a particular genotype will survive & reproduce

(3) Each genotypic class makes a relative contribution to the next generation,
        which is proportional to its initial frequency, weighted by its fitness.

    [e.g., if the AA genotype has a frequency of 0.25 and 80% survive to reproduce,
             the relative contribution of AA to the next generation is (0.25)(0.8)=0.20]

    The sum of the relative contributions of all three genotypes is

(read as, "W bar") = mean population fitness
In this simple model,

< 1, because not all individuals on Line (1) survive.

(4) Because

< 1, the surviving genotypic contributions have to be "normalized ":
Dividing the proportion of each genotype by

returns the sum to unity,
& the final values are the relative genotype frequencies after selection.

To derive the allele frequencies after selection,
take Line (4) above and recall q = f(BB) + (1/2) f(AB)

so q' = q²W₂/

+ (1/2) 2pqW₁/

= q(qW₂ + pW₁)/

then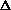

q = q' - q = q_after - q_before = q(qW₂ + pW₁)/

- q

= [(q)(qW₂ + pW₁) - (q)(p²W₀ + 2pqW₁ + q²W₂)] /

[Note 1]

= [(q)(qW₂ + pW₁ - p²W₀ - 2pqW₁ - q²W₂)] /

[Note 2]

= [(q)(pqW₂ + W₁p(1-2q) - pW₀p)] /

[Note 3]

= [(pq)(qW₂ + W₁(1-2q) - W₀p)] /

[Note 4]

= [(pq)(W₂q + W₁(p-q) - W₀p)] /

[Note 5]

= [(pq)(W₂q + W₁p - W₁q - W₀p)/

[Note 6]

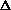q = [pq] [(q)(W₂- W₁) + (p)(W₁ - W₀)] / []
________________________________________________

Notes:
[1] Expand

in numerator, from Line 4 of Table
[2] Combine terms by factoring out q from

[3] trick: Combine W₂ terms by noting (q - q²) = (q)(1 - q) = pq
[4] Factor out p from W₀, W₁, & W₂ terms
[5] trick: (1 - 2q) = (1 - q) - q = (p - q)
[6] Expand W₁ term, gather p & q terms

Homework : Repeat the derivation of the model for in terms of the other allele,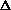

p = p' - p