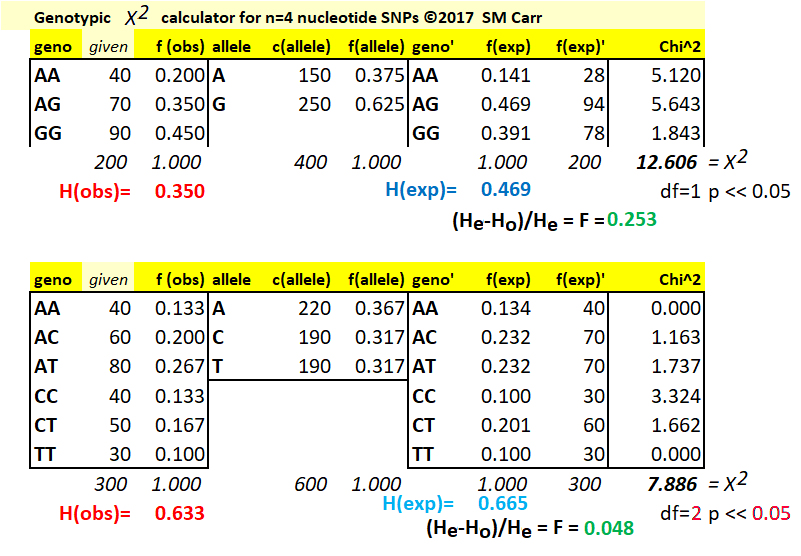
The Chi-Square Test for Hardy-Weinberg Genotype Proportions
(1) For a
locus with an A/G SNP polymorphisms, given
the observed genotype counts that total to 200, the f(obs)
of each genotype is (given) / (total). The count of alleles c(alleles)
is then two for each homozygote plus one for
each heterozygote, for example c(A) = (2)(40) + 70 =
150. Noting that the number of alleles is twice the number of
genotypes, the frequency of alleles f(allele) is f(A)
= 150 / 400 = 0.375. Then, f(G) = 250 / 400 = 0.625
or (1 - f(A)) = (1 - 0.375). Calculate
the expected genotype frequencies
from these observed allele frequencies: if p =
f(A) and q = f(G), then p2
= f(AA), 2pq = f(AG),
and q2 = f(GG).
Expected genotype counts in each case are then (frequency)
X (total observed).
[BTW: The Inbreeding Coefficient (F) can be calculated as this point from knowledge of the observed heterozygosity (0.350) and the expected heterozygosity (calculated as (2) (0.375)(0.625) = 0.469, thus F = (0.350 - 0.469) / 0.469 = 0.253].
Calculate the Chi-Square value (X2) contributed by each genotype as the difference between the observed and expected counts, divided by the expected count, quantity squared: for AA, (AAobs - AAexp)2 / (AAexp) = (40 - 28)2 / (40) = 5.120. Repeat this calculation for each genotype, and sum the total, which is the Chi-Square value for the test, in this case 12.606.
To evaluate the statistical significance of this value, it is necessary to know the number of degrees of freedom (df) in the experimental data, which is reported and evaluated along with the result. In general, the d.f. of any experiment is one less than the number of categories compared, (n-1). In general, if you have n experimental results that could have fallen into any of three categories a b c, the value of the first category a can be anything up to n, and the value of the second category b can be anything up to (n-a). Having determined a and b, the third value is now pre-determined: c = (n - a - b). So, only two of the values are free to vary.
For diploid genotypic data with two alleles A & G and three genotypes AA, AG, & GG, this might suggest df = 2. However, if we know f(G) = q, then f(A) = (1-q), and f(AA) = (1-q)2, f(AG) = (2)(1-q)(q) and f(GG) = q2. Thus, the expected values of the three genotype categories are pre-determined by knowledge of one of the allele frequencies q, which determines the other, and therefore df = 1. In general, for nucleotide or other allelic data, df = n-1 where n = # of alleles.
(2) The same principles apply to calculations for the C / A / T SNP polymorphism. Note that the counts of alleles will involved three heterozygote classes each. Note the calculation of heterozygosity can be done either adding the frequency of the (three) heterozygote classes directly, or by adding the frequencies of the (three) homozygotes and subtracting the total from 1. However, as the number of alleles increases, becomes computationally more efficient to use the latter calculation
Two further points.
(3) Calculation of expected genotype counts from frequency data may result in the expectation of a 'fractional individual,' which makes no mathematical biological sense. If we were testing for a 3:1 genotypic ratio among 17 individuals, we cannot expect to see 12.75 and 4.25, so we round the expected values to the closest integer, here 13 and 4, which still adds to 17. This is applicable to the multiple-category data above. A related problem arises when, among 18 individuals, calculated expectations are 13.5 and 4.5: if we round both to 13 and 4, we are shy one expected and the test calculation is biased. One convention is to round one or the other expectation up, in the same trend seen in the data. That is, if we have a 3:1 hypothesis and observe 15 & 3, we round the expectations to 14 & 4. If we observed 12 & 6, we round the expectation to 13 & 5. These corrections reduce the possibility of obtaining a significant result due to a computational bias, and increases validity of the result.
(4) Chi-square calculations must be performed with count data, not frequencies or percentages. Because it squares the magnitude of the deviation, X2 values are heavily influenced by the absolute magnitude of the numbers. For 0.6 & 0.4 observed versus 0.5 & 0.5 expected, X2 = 0.12 / 0.5 + (-0.1)2 / 0.5 = 0.02 / 0.5 = 0.04 ns, whereas with 60 & 40 versus 50 & 50 expected, X2 = 102 / 50 + (-10)2 / 50 = 200 / 50 = 4.0* , and with 600 & 400 versus 500 & 500 expected X2 = 1002 / 500 + (-100)2 / 500 = 20,000 / 500 = 40.0***. The proportional deviation is the same in each case (20%), but when the actual deviation is squared, and contributes much for strongly to X2 as n increases. This is also a reminder that larger samples sizes produce more sensitive experiments.
,[BTW: The Inbreeding Coefficient (F) can be calculated as this point from knowledge of the observed heterozygosity (0.350) and the expected heterozygosity (calculated as (2) (0.375)(0.625) = 0.469, thus F = (0.350 - 0.469) / 0.469 = 0.253].
Calculate the Chi-Square value (X2) contributed by each genotype as the difference between the observed and expected counts, divided by the expected count, quantity squared: for AA, (AAobs - AAexp)2 / (AAexp) = (40 - 28)2 / (40) = 5.120. Repeat this calculation for each genotype, and sum the total, which is the Chi-Square value for the test, in this case 12.606.
To evaluate the statistical significance of this value, it is necessary to know the number of degrees of freedom (df) in the experimental data, which is reported and evaluated along with the result. In general, the d.f. of any experiment is one less than the number of categories compared, (n-1). In general, if you have n experimental results that could have fallen into any of three categories a b c, the value of the first category a can be anything up to n, and the value of the second category b can be anything up to (n-a). Having determined a and b, the third value is now pre-determined: c = (n - a - b). So, only two of the values are free to vary.
For diploid genotypic data with two alleles A & G and three genotypes AA, AG, & GG, this might suggest df = 2. However, if we know f(G) = q, then f(A) = (1-q), and f(AA) = (1-q)2, f(AG) = (2)(1-q)(q) and f(GG) = q2. Thus, the expected values of the three genotype categories are pre-determined by knowledge of one of the allele frequencies q, which determines the other, and therefore df = 1. In general, for nucleotide or other allelic data, df = n-1 where n = # of alleles.
(2) The same principles apply to calculations for the C / A / T SNP polymorphism. Note that the counts of alleles will involved three heterozygote classes each. Note the calculation of heterozygosity can be done either adding the frequency of the (three) heterozygote classes directly, or by adding the frequencies of the (three) homozygotes and subtracting the total from 1. However, as the number of alleles increases, becomes computationally more efficient to use the latter calculation
Two further points.
(3) Calculation of expected genotype counts from frequency data may result in the expectation of a 'fractional individual,' which makes no mathematical biological sense. If we were testing for a 3:1 genotypic ratio among 17 individuals, we cannot expect to see 12.75 and 4.25, so we round the expected values to the closest integer, here 13 and 4, which still adds to 17. This is applicable to the multiple-category data above. A related problem arises when, among 18 individuals, calculated expectations are 13.5 and 4.5: if we round both to 13 and 4, we are shy one expected and the test calculation is biased. One convention is to round one or the other expectation up, in the same trend seen in the data. That is, if we have a 3:1 hypothesis and observe 15 & 3, we round the expectations to 14 & 4. If we observed 12 & 6, we round the expectation to 13 & 5. These corrections reduce the possibility of obtaining a significant result due to a computational bias, and increases validity of the result.
(4) Chi-square calculations must be performed with count data, not frequencies or percentages. Because it squares the magnitude of the deviation, X2 values are heavily influenced by the absolute magnitude of the numbers. For 0.6 & 0.4 observed versus 0.5 & 0.5 expected, X2 = 0.12 / 0.5 + (-0.1)2 / 0.5 = 0.02 / 0.5 = 0.04 ns, whereas with 60 & 40 versus 50 & 50 expected, X2 = 102 / 50 + (-10)2 / 50 = 200 / 50 = 4.0* , and with 600 & 400 versus 500 & 500 expected X2 = 1002 / 500 + (-100)2 / 500 = 20,000 / 500 = 40.0***. The proportional deviation is the same in each case (20%), but when the actual deviation is squared, and contributes much for strongly to X2 as n increases. This is also a reminder that larger samples sizes produce more sensitive experiments.
Text material © 2019 by Steven M. Carr