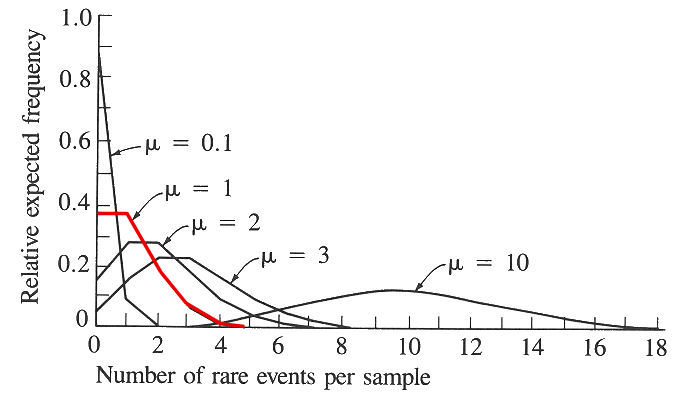

The Poisson distribution is a modified
form of the binomial distribution that is useful for the analysis of
phenomena characterized by discrete, rare events. For example, in a
study of the distribution of a rare plant among a number of quadrats, a
majority of plots may contain no specimens, a
smaller number a single plant, and still smaller numbers two, three,
or more plants. If a single plant per quadrat is expected, the mean µ = 1
and the "0" and "1" classes occur at 37% each, the "2" class at 18%, the "3"
class at 6%, and larger classes take up the remaining 2%. The
characteristic test for a Poisson is that the variance
equals the mean, which
in the plant example means that the rare plant is randomly
distributed. Note, that, In the distributions above, as the mean µ increases towards 10, the distribution approaches normality.
The Poisson may be used to evaluate whether events
occur independently in time as well as space. In a classic example, Bortkiewicz (1898) studied the
distribution of 122 men kicked to death by horses among ten Prussian
army corps over 20 years. In most years in most corps, no one dies from being kicked; in one corp in one year, four men
were kicked to death. Does this mean something was amiss in this particular corp? Analysis indicates that the
observed frequencies conform quite closely to the expected Poisson
frequencies, and that the mean and variance are
almost identical, as expected. The corp was just "unlucky" in the
sense that it is in the extreme tail of an ordinary run of events.
Number of men kicked to death by horses in ten Prussian army corps
| # men killed / year / corp |
Observation (# deaths) |
Poisson Expectation |
| 0 |
109 (0) |
108.7 (0.0) |
| 1 |
65 (65) |
66.3 (66.3) |
| 2 |
22 (44) |
20.2 (40.4) |
| 3 |
3 (9) |
4.1 (12.3) |
| 4 |
1 (4) |
0.6 (2.4) |
| 5+ |
0 (0) |
0.1 (0.5) |
| # corp-years |
200 |
200.0 |
| Total deaths |
122 |
121.9 |
| Mean |
0.610 |
0.610 |
| Variance |
0.611 |
0.610 |