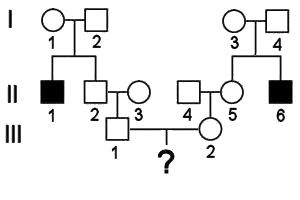
Calculating probability and risks in pedigree analysis:
Elementary principles
The pedigree
shows the occurrence of an autosomal
recessive trait, where the black squares have
genotype aa.
We wish to calculate the probability that IV-1 (shown as ?) will be either
affected (aa), or a
carrier heterozygote (Aa).
(1) For IV-1 to be an affected recessive homozygote, s/he must inherit an a allele from the father and the mother. Given that II-1 must be aa, both great-grandparents (I-1 and I-2) must be Aa. II-2 shows the dominant phenotype, and therefore has at least one A allele: the probability that the other is a is 1/2. II-3 is from outside the affected pedigree and can be assumed to be AA. Like his father, III-1 shows the dominant phenotype, and therefore has at least one A. Then, the probability that III-1 is Aa is the probability that II-2 is heterozygous and passed the a allele to III-1 : (1/2) x (1/2) = 1/4. The same reasoning leads to the conclusion that III-2 is heterozygous with a probability of 1/4. Thus, for IV-1 to be aa, both parents must be Aa, and they must both pass the a allele to their offspring: 1/4 x 1/4 x 1/4 = 1/64
(2) Alternatively, for IV-1 to be a heterozygous, carrier, either s/he most inherit an a allele from the father, or from the mother. The chance of either parent being a heterozygote is 1/4, as calculated above. Then, the probability that both parents are heterozygotes, and the probability that two heterozygotes will have a heterozygous child, is 1/4 x 1/4 x 1/2 = 1/32.
(3) Finally, the probability that IV-1 is a dominant homozygote is 1 - 1/64 - 1/32 = (64 - 1 - 2)/64 = 61/64. This can also be calculated more tediously by summing the alternative probabilities at each of the steps above.
The calculations in this example involved a distinction between a priori and a posteriori probability, which are often presented incorrectly in elementary genetics textbooks. To take a simple case: the a priori probability of getting heads on a single toss of a penny is 1/2, since there are two equal possibilities, H or T. Then, given two pennies tossed at random, HH, HT, TH, and TT are all equally likely. The a priori probability of getting at least one head is 3/4. The a priori probability that any combination with at least one head will have two tails (HT or TH vs HH) is 2/3.
However, consider an experiment in which I have tossed two pennies. I show you that one is H, and ask, What is the probability that the other is also H? The a posteriori probability is 1/2 : given the knowledge that one coin is H, the other is H or T with equal probability. In anticipation of the experiment, the a priori probability of HT given H- is 2/3. In analyzing the results of any particular experiment, the added information changes probabilities a posteriori.
In the above example, we know that I-1 and I-2 are heterozygotes and II-2 shows the dominant phenotype. We therefore know a posteriori that he has inherited a dominant alleles from one parent, and the probability that he will inherit a recessive alleles from the other parent and be heterozygous is 1/2. It is incorrect to reason that, since 2/3 of all unaffected children (that is, all non-aa) are heterozygotes a priori, his individual risk is also 2/3. Stated another way, by knowing the nature of one allele, we have lost one statistical degree of freedom.
[In the simplest case: the probability that the next child of I-1 and I-2 will be a boy is a priori 1/2: once the child is born, the probability a posterior is either 0 or 1].
Two further extensions of this idea. For this scenario, assume that a genetic test is available to distinguish AA from Aa, but II-5 is deceased and III-2 will not take the test.
(4) Suppose III-2 has a heterozygous sibling. How does this change the calculation IV-I's risk? This would mean that II-5 must be a heterozygote with a probability of 1, not 1/2 as before. Then, the probability that III-2 is a heterozygote is 1/2, the probability that the father (III-1) is a heterozygote remains 1/4, and the probability that IV-1 is aa is 1/2 x 1/4 x 1/4 = 1/32.
(5) Suppose III-2 has one or more siblings who test as unaffected homozygotes (AA). How does this change the calculation of IV-1's risk? Note that, whereas the birth of a heterozygous sibling proves that the mother (II-5) is a heterozygote, the birth of unaffected homozygous offspring cannot prove that she is a homozygote. However, multiple births of unaffected siblings do decrease the probability that she is a heterozygote, as follows. The probability that a heterozygote will not pass the a allele to an offspring is 1/2. Then, the probability that she will not pass it to either of two offspring is (1/2)(1/2) = 0.52 = 1/4. The probability that she will pass it to none of three offspring is 0.53 = 1/8, to none of four is 1/16, and so on. Less than 0.1% of all families with ten children would have known with an a alleles, if II-5 were a heterozygote. In other words, this is strong a posteriori evidence that II-5 is a homozygote, which if true means that IV-1 cannot be affected. Of course, the birth of an eleventh child who is Aa immediately proves that II-5 is heterozygous, and returns IV-1's risk calculation to 1/16, as in (4) above..
(1) For IV-1 to be an affected recessive homozygote, s/he must inherit an a allele from the father and the mother. Given that II-1 must be aa, both great-grandparents (I-1 and I-2) must be Aa. II-2 shows the dominant phenotype, and therefore has at least one A allele: the probability that the other is a is 1/2. II-3 is from outside the affected pedigree and can be assumed to be AA. Like his father, III-1 shows the dominant phenotype, and therefore has at least one A. Then, the probability that III-1 is Aa is the probability that II-2 is heterozygous and passed the a allele to III-1 : (1/2) x (1/2) = 1/4. The same reasoning leads to the conclusion that III-2 is heterozygous with a probability of 1/4. Thus, for IV-1 to be aa, both parents must be Aa, and they must both pass the a allele to their offspring: 1/4 x 1/4 x 1/4 = 1/64
(2) Alternatively, for IV-1 to be a heterozygous, carrier, either s/he most inherit an a allele from the father, or from the mother. The chance of either parent being a heterozygote is 1/4, as calculated above. Then, the probability that both parents are heterozygotes, and the probability that two heterozygotes will have a heterozygous child, is 1/4 x 1/4 x 1/2 = 1/32.
(3) Finally, the probability that IV-1 is a dominant homozygote is 1 - 1/64 - 1/32 = (64 - 1 - 2)/64 = 61/64. This can also be calculated more tediously by summing the alternative probabilities at each of the steps above.
The calculations in this example involved a distinction between a priori and a posteriori probability, which are often presented incorrectly in elementary genetics textbooks. To take a simple case: the a priori probability of getting heads on a single toss of a penny is 1/2, since there are two equal possibilities, H or T. Then, given two pennies tossed at random, HH, HT, TH, and TT are all equally likely. The a priori probability of getting at least one head is 3/4. The a priori probability that any combination with at least one head will have two tails (HT or TH vs HH) is 2/3.
However, consider an experiment in which I have tossed two pennies. I show you that one is H, and ask, What is the probability that the other is also H? The a posteriori probability is 1/2 : given the knowledge that one coin is H, the other is H or T with equal probability. In anticipation of the experiment, the a priori probability of HT given H- is 2/3. In analyzing the results of any particular experiment, the added information changes probabilities a posteriori.
In the above example, we know that I-1 and I-2 are heterozygotes and II-2 shows the dominant phenotype. We therefore know a posteriori that he has inherited a dominant alleles from one parent, and the probability that he will inherit a recessive alleles from the other parent and be heterozygous is 1/2. It is incorrect to reason that, since 2/3 of all unaffected children (that is, all non-aa) are heterozygotes a priori, his individual risk is also 2/3. Stated another way, by knowing the nature of one allele, we have lost one statistical degree of freedom.
[In the simplest case: the probability that the next child of I-1 and I-2 will be a boy is a priori 1/2: once the child is born, the probability a posterior is either 0 or 1].
Two further extensions of this idea. For this scenario, assume that a genetic test is available to distinguish AA from Aa, but II-5 is deceased and III-2 will not take the test.
(4) Suppose III-2 has a heterozygous sibling. How does this change the calculation IV-I's risk? This would mean that II-5 must be a heterozygote with a probability of 1, not 1/2 as before. Then, the probability that III-2 is a heterozygote is 1/2, the probability that the father (III-1) is a heterozygote remains 1/4, and the probability that IV-1 is aa is 1/2 x 1/4 x 1/4 = 1/32.
(5) Suppose III-2 has one or more siblings who test as unaffected homozygotes (AA). How does this change the calculation of IV-1's risk? Note that, whereas the birth of a heterozygous sibling proves that the mother (II-5) is a heterozygote, the birth of unaffected homozygous offspring cannot prove that she is a homozygote. However, multiple births of unaffected siblings do decrease the probability that she is a heterozygote, as follows. The probability that a heterozygote will not pass the a allele to an offspring is 1/2. Then, the probability that she will not pass it to either of two offspring is (1/2)(1/2) = 0.52 = 1/4. The probability that she will pass it to none of three offspring is 0.53 = 1/8, to none of four is 1/16, and so on. Less than 0.1% of all families with ten children would have known with an a alleles, if II-5 were a heterozygote. In other words, this is strong a posteriori evidence that II-5 is a homozygote, which if true means that IV-1 cannot be affected. Of course, the birth of an eleventh child who is Aa immediately proves that II-5 is heterozygous, and returns IV-1's risk calculation to 1/16, as in (4) above..