Measures of central tendency and dispersion
Biological phenomena can often be described by a measure of central tendency (the average, or arithmetic mean), and a measure of dispersion (variance). To express dispersion in terms of magnitude without regard to sign, the difference from the mean is squared. To express dispersion in the same units as the mean, the square root of the variance is the standard deviation.
Mean = sum of i individual values of variable X, divided by number of individuals N
=
(xi) / N = 
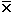[read as, "X bar"]
= (x1 + x2 + x3 + ... xn) / N
Variance = average squared deviation of individuals from the mean
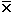= (1 / N) (xi - )2 =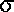 
2 [read as, "sigma squared"]
computationally, this is more easily calculated as
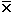= (1 / N) (xi2) - 2
which formula can be remembered as
= "mean of squares" minus "square of means" [MOSSOM]
Standard deviation = square root of variance
s = (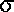2)1/2
Biological phenomena can often be described by a measure of central tendency (the average, or arithmetic mean), and a measure of dispersion (variance). To express dispersion in terms of magnitude without regard to sign, the difference from the mean is squared. To express dispersion in the same units as the mean, the square root of the variance is the standard deviation.
Mean = sum of i individual values of variable X, divided by number of individuals N
=
(xi) / N = 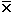[read as, "X bar"]= (x1 + x2 + x3 + ... xn) / N
Variance = average squared deviation of individuals from the mean
= (1 / N)
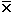(xi - )2 = 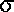2 [read as, "sigma squared"]computationally, this is more easily calculated as
= (1 / N)
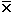(xi2) - 2which formula can be remembered as
= "mean of squares" minus "square of means" [MOSSOM]
Standard deviation = square root of variance
s = (
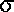2)1/2