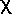 2)
test
2)
test The critical
value for a single-classification
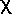 2 test
("either / or": observed
and expected values are either one way or the other), therefore with degrees of freedom = df = 1 is
3.84 at p = 0.05. That is, for
a test of a
hypothesis with two equally-likely alternative
outcomes (heads or tails, round or wrinkled, left or
right, etc),
2 test
("either / or": observed
and expected values are either one way or the other), therefore with degrees of freedom = df = 1 is
3.84 at p = 0.05. That is, for
a test of a
hypothesis with two equally-likely alternative
outcomes (heads or tails, round or wrinkled, left or
right, etc), 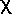 2 = 3.84 or greater indicates that the chances
are 5% or less that so large a deviation could have been
obtained simply by chance. [Alternatively, in a large
number of similar experiments, such a result would occur
about one time in 20]. Given a
2 = 3.84 or greater indicates that the chances
are 5% or less that so large a deviation could have been
obtained simply by chance. [Alternatively, in a large
number of similar experiments, such a result would occur
about one time in 20]. Given a 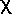 2
= 6.635
or greater, the chance is less than 1%. A
statistical outcome that occurs less than 5% of
the time is said to be significant marked
and *; a results obtained
less than 1% of the time is highly
significant and marked **.
Non-significant outcomes are marked ns.
2
= 6.635
or greater, the chance is less than 1%. A
statistical outcome that occurs less than 5% of
the time is said to be significant marked
and *; a results obtained
less than 1% of the time is highly
significant and marked **.
Non-significant outcomes are marked ns.
The formula for the calculation for a single-classification test is as follows, where w + z = x + y, the deviation (d) is the difference between the observed (o) and expected (e) results for each class, and the chi-square value* is the squared deviation divided by the expected value, summed for both classes:
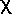 2 =
2 =  [d2/e] = [(x-w)2
/ w] + [(y-z)2 / z]
[d2/e] = [(x-w)2
/ w] + [(y-z)2 / z]
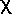 2 = 1/5 + 1/5 = 0.40, ns
2 = 1/5 + 1/5 = 0.40, ns
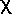 2 = 3.84 or greater indicates that the chances
are 5% or less that so large a deviation could have been
obtained simply by chance. [Alternatively, in a large
number of similar experiments, such a result would occur
about one time in 20]. Given a
2 = 3.84 or greater indicates that the chances
are 5% or less that so large a deviation could have been
obtained simply by chance. [Alternatively, in a large
number of similar experiments, such a result would occur
about one time in 20]. Given a 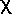 2
= 6.635
or greater, the chance is less than 1%. A
statistical outcome that occurs less than 5% of
the time is said to be significant marked
and *; a results obtained
less than 1% of the time is highly
significant and marked **.
Non-significant outcomes are marked ns.
2
= 6.635
or greater, the chance is less than 1%. A
statistical outcome that occurs less than 5% of
the time is said to be significant marked
and *; a results obtained
less than 1% of the time is highly
significant and marked **.
Non-significant outcomes are marked ns.
The formula for the calculation for a single-classification test is as follows, where w + z = x + y, the deviation (d) is the difference between the observed (o) and expected (e) results for each class, and the chi-square value* is the squared deviation divided by the expected value, summed for both classes:
| o |
e |
d |
d2/e |
|
| I |
x |
w |
(x-w) |
(x-w)2 / w |
| II |
y |
z |
(y-z) |
(y-z)2 / z |
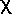 2 =
2 =  [d2/e] = [(x-w)2
/ w] + [(y-z)2 / z]
[d2/e] = [(x-w)2
/ w] + [(y-z)2 / z]Consider
two experiments in which coins are tossed, and the two
possibilities are heads (H)
or tails (T). The
first involves n = 10
tosses, the second n = 100
tosses
| o |
e |
d |
d2/e |
|
| H |
6 |
5 |
1 |
1 / 5 |
| T |
4 |
5 |
-1 |
1 / 5 |
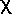 2 = 1/5 + 1/5 = 0.40, ns
2 = 1/5 + 1/5 = 0.40, ns| o |
e |
d |
d2/e |
|
| H |
60 |
50 |
10 |
100 /
50 |
| T |
40 |
50 |
-10 |
100 /
50 |
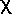 2 = 2.0 + 2.0
= 4.0*,
p < 0.05 [or 0.05 > p > 0.01]
2 = 2.0 + 2.0
= 4.0*,
p < 0.05 [or 0.05 > p > 0.01]Note that the same 60% / 40% proportion is not significantly different from random in the smaller experiment, but is significant in the larger. This emphasizes that actual numbers, not proportions, must be tested, and that statistical power (ability to detect a difference of a particular magnitude) is greater in larger experiments.
*For the advanced student: show that, for a single-classification test with a total sample size of n where X is the value of the first observed class and the two expected values are equal or "even" (x = y = 0.5), the value of chi-square simplifies to